Marion, eine Leserin, auf deren Blog ich schon mehr als einmal als Gastautorin gewirkt habe, schickte mir neulich einen Link zu einem Video, das gerade auf Facebook die Runde machte. Darin zu sehen sind Einwohner Kenias bzw. Tansanias, die filmenden Touristen ein Experiment vorführen. Das Spannende daran: Diese beiden Länder liegen auf dem Äquator!
Die Anrainer dieser Kreislinie, welche den Globus genau in Nord- und Südhalbkugel teilt, möchten den Touristen mit ihrem Experiment weismachen, dass Wasser, welches durch ein enges Loch abläuft, je nach Position auf der Erdkugel in eine bestimmte Richtung wirbelt: Links herum auf der Nordhalbkugel, Rechts herum auf der Südhalbkugel und genau auf dem Äquator ganz ohne Wirbel, d.h. gerade nach unten durch das Loch. Und das soll mit Hilfe eines Trichters und eines Eimers Wasser auf einem vielleicht 30 Meter langen Stück Strasse nachprüfbar sein.
„Das ist doch alles fake, oder?“, fragte mich die Leserin. Und mein Instinkt sagte gleich, dass ihrem Bauchgefühl zu trauen sei. Dennoch habe ich nachgelesen und schnell bestätigt bekommen – unter anderem in der Lehrmaterialsammlung der Uni Karlsruhe – dass Marion ganz richtig liegt: Alles fake!
Aber wie kommt es dazu, dass derlei Gerüchte um die Drehrichtung von abfliessendem Wasser sich so hartnäckig um die ganze Welt verbreiten (auch in südamerikanischen Ländern auf dem Äquator sollen entsprechende Experimente gezeigt werden)? Warum sollte das Wasser auf der Nordhalbkugel links- und auf der Südhalbkugel rechtsherum in den Abfluss wirbeln?
Was die Drehrichtung des Wassers bestimmen soll: Die Corioliskraft
Urheber der vorbestimmten Drehrichtung sei – so heisst es in den meisten Gerüchten – die Drehbewegung der Erde um sich selbst. Die führt nämlich wirklich dazu, dass eine geheimnisvolle Kraft – die Physiker nennen sie Corioliskraft – von der Erdkugel ausgehende Bewegungen in eine bestimmte Richtung ablenkt!
Welche Bewegungen werden abgelenkt?
Die Corioliskraft wirkt auf solche Bewegungen, die von einem Pol zum anderen, also entlang der Längengrade (jener Linien, die auf der Weltkarte oder dem Globus Nord- und Südpol miteinander verbinden) oder von der Drehachse der Erde fort bzw. zu ihr hin (aus Sicht eines Menschen auf der Erdoberfläche „nach oben“ oder „nach unten“ verlaufen.
Wie kommt es zu der Ablenkung?
Die Erdumdrehung als Ursache
Die Erde ist (mehr oder weniger) eine Kugel, die sich stetig um ihre Mittelachse dreht – also um die gerade Linie, die Nord- und Südpol durch die Kugel hindurch miteinander verbindet. Da diese Erdkugel im Grossen und Ganzen ein fester Körper ist, müssen sich alles Material, aus dem sie besteht und alles, was sonst noch darauf haftet (Meere, Pflanzen, Tiere, Menschen und sogar die Lufthülle, die den Planeten umgibt!) stets im gleicher Lage zueinander mitdrehen, damit alles seinen Platz behält. Schliesslich ist es noch nie vorgekommen, dass jemand seine Fortbewegung durch die Erddrehung verschlafen hätte und ein paar Tausend Kilometer weiter westlich wieder aufgewacht wäre.
Alle Orte auf der Erde drehen sich gemeinsam
Dieser feste Zusammenhalt aller Teile der Erdkugel führt auch dazu, dass die Entfernung zwischen Tunis, der Hauptstadt Tunesiens in Nordafrika, und der Norwegischen Hauptstadt Oslo zu jeder Tages- und Nachtzeit gleich ist. Wenn ihr nun Tunis und Oslo auf einem Globus-Modell ausfindig macht (beide Städte liegen nahezu auf demselben Längengrad!) und kleines Bisschen von Physik versteht, mag euch eine Ungereimtheit ins Auge fallen:
Nicht alle Punkte auf der Erdoberfläche drehen sich gleich schnell
Tunis liegt deutlich weiter aussen auf der Wölbung des Globus‘ als Oslo, d.h. der Abstand von Tunis zur Mittelachse ist deutlich grösser als der Abstand von Oslo zur Mittelachse. Das bedeutet, dass der Kreis, welchen Tunis innerhalb eines Tages entlang bewegt wird, erheblich länger ist – d.h. einen grösseren Umfang hat – als der Kreis, welchen Oslo entlang bewegt wird!
Vom Abstand zum Kreisumfang
Die Länge einer Kreislinie, d.h. den Umfang U eines Kreises kann man berechnen, indem man seinen Radius r – den Abstand zwischen Kreislinie und Kreismittelpunkt – mit 2 und der Zahl Pi multipliziert.
Damit entspricht der (kürzeste) Abstand von Tunis bzw. Oslo zur Drehachse der Erde dem Radius, aus dem sich die Länge des Umlaufs der jeweiligen Stadt während eines Tages ergibt.
Damit die Entfernung zwischen beiden Städten stets gleich bleibt, müssen sowohl Tunis als auch Oslo sich an einem Tag (d.h. in 24 Stunden) genau einmal um die Erdachse wandern. Wegen des grösseren Abstands zur Drehachse muss Tunis dazu einen längeren Weg zurücklegen als Oslo. Das bedeutet: Tunis muss sich schneller bewegen als Oslo, um seine längere Umlaufstrecke am gleichen Tag zu schaffen!
Geschwindigkeit und Drehgeschwindigkeit
Die Geschwindigkeit v einer gleichförmigen, d.h. stetig in die gleiche Richtung verlaufenden Bewegung kann man ausrechnen, indem man einen zurückgelegten Streckenabschnitt durch die dafür benötigte Zeitspanne teilt:
Eine vergleichbare Beziehung gilt auch für eine gleichförmige Kreisbewegung, in welcher der zurückgelegte Winkel Phi (φ) den Streckenabschnitt ersetzt. Die so berechnete Grösse nennen die Physiker Dreh- oder Winkelgeschwindigkeit und schreiben dafür statt v ein kleines Omega (ω):
Wenn die benötigte Zeit für zwei Bewegungen gleich ist, aber ein Streckenabschnitt bzw. Winkel grösser als der andere, ergibt sich mit dem somit grösseren Zähler im Bruch auf der rechten Seite der Gleichung aus dem grösseren Streckenabschnitt bzw. Winkel eine grössere Geschwindigkeit.
Gut sichtbar wird das, wenn ihr euch die Erdkugel einmal von „oben“ anseht:
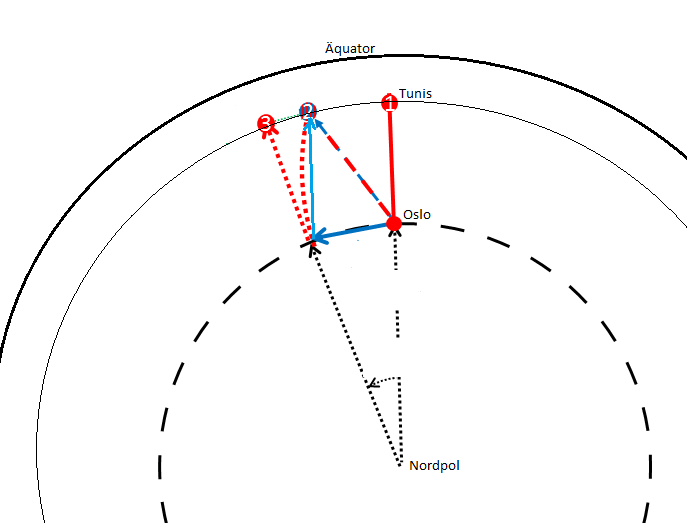
Die Erde von einem Punkt über dem Nordpol aus gesehen: Die Nordhalbkugel erscheint als flache Scheibe mit dem Nordpol als Mittelpunkt. Ein Fussball fliegt von Oslo in der Nähe des Mittelpunkts nach Tunis, welches weiter vom Mittelpunkt entfernt liegt. Aus der Summe der Geschwindigkeiten von Oslo (kurzer blauer Pfeil) und der Südwärtsbewegung des Balles (durchgezogener roter bzw. langer blauer Pfeil) ergibt sich Punkt (2) als Zielpunkt für den Ball. Tunis, das sich schneller als Oslo bewegen muss, um seinen längeren Kreisabschnitt in gleicher Zeit zu schaffen, befindet sich dann aber schon an Punkt (3)! Der Weg des Balls kann auch durch die gekrümmte gepunktete Linie beschrieben werden: Eine Kraft – die Corioliskraft, die nach „rechts“ wirkt, lenkt den Ball von der geraden Flugbahn ab.
Die Grafik zeigt die Erde aus der Sicht eines Astronauten, der über dem Nordpol (in der Grafik der Mittelpunkt der Kreise) schwebt. Die gestrichelte Kreisline markiert den Weg, auf dem sich Oslo mit der Erde dreht. Die mittlere, durchgezogene Kreislinie zeigt den Weg, den Tunis nimmt (da Tunis auf der Kugelwölbung weiter aussen liegt, ist dieser Kreis grösser). Der ganz äussere Kreis ist der Äquator – die Südhalbkugel ist aus dieser Richtung nicht zu sehen.
Ein Fussballspiel von Oslo nach Tunis
Stellt euch nun vor, ein besonders kräftiger Spieler würde einen Fussball vom Anstosspunkt im Osloer Stadion über die Stadionmauer in Richtung Tunis (also genau nach Süden) treten. Wenn der Fussballspieler nun als Kind in den Zaubertrank gefallen ist und der Ball seine Reise über Europa hinweg antritt…wo würde er dann – die Lufthülle der Erde mal ausser Acht gelassen – landen? Im Tor im Stadion von Tunis?
Die Krux mit der Impulserhaltung
Eines der grundlegenden Gesetze der Physik – das Gesetz der Impulserhaltung – schreibt vor, dass jede Bewegung eines jeden Gegenstands in jede Richtung erhalten bleibt, so lange keine Kraft in die der Bewegung entgegengesetzte Richtung wirkt und ihn ausbremst.
Da der Fussball vor dem Anstoss auf der Erde gelegen hat, hat er sich zunächst mit der Geschwindikgeit von Oslo um die Erdachse gedreht. Diese Drehrichtung und -geschwindigkeit bleibt dem Ball auch, nachdem der Fussballer ihn in Richtung Süden getreten hat. Die Bewegung in Richtung Süden wird einfach zur Bewegung in Richtung der Oslo-Kreisbahn hinzugezählt.
Wie man Bewegungen addiert
Die geraden Pfeile in der Grafik zeigen die Richtungen der Teilbewegungen an – die Länge der Pfeile steht für die Geschwindigkeit bzw. den Impuls in der jeweiligen Richtung. Verschiebt man nun das hintere Ende eines Pfeils an die Spitze des ersten, zeigt der neue Pfeil vom hinteren Ende des einen zur Spitze des anderen Pfeils die Richtung der Gesamtbewegung (und dessen Länge die Gesamtgeschwindigkeit). Dieses Verfahren nennen die Mathematiker Vektoraddition (denn die Pfeile heissen bei ihnen Vektoren).
Die Grafik zeigt: Obwohl nach Süden getreten bewegt sich der Fussball diagonal über Europa nach Südosten – wobei die Geschwindikeit in Ost-Richtung der von Oslo entspricht. Damit landet der Ball am Punkt 2 irgendwo an der tunesischen oder algerischen Mittelmeerküste und nicht in Tunis (das befindet sich inzwischen weiter östlich an Punkt 3). Denn weil Tunis sich schneller bewegt als Oslo, ist es während der Flugzeit des Fussballs weiter nach Osten gewandert als der von der Impulserhaltung als „südlich von Oslo“ vorgegebene Punkt 2! Der Schuss geht also gründlich daneben.
Durch Drehbewegung auf die krumme Bahn
Wenn der Astronaut, der über dem Nordpol unbewegt schwebt, dieses unglaubliche Fussballspiel beobachtet und filmt, um anschliessend die Position des Balles in regelmässigen Zeitabschnitten einzublenden, erhält er eine Linie, die dem nach links gekrümmten gestrichelten Pfeil in der Grafik entspricht. Solch eine gekrümmte Flugbahn lässt sich mathematisch beschreiben, indem man annimmt, dass eine Kraft den Fussball in Ablenkungsrichtung beschleunigt – die sogenannte Corioliskraft.
Kraft und Beschleunigung: Zwei physikalische Grössen mit Richtung
Das Grundgesetz der Mechanik beschreibt die einfache Beziehung zwischen Kraft (F) und Beschleunigung (a):
Je grösser die Kraft ist, die auf einen Gegenstand mit der Masse m wirkt, desto grösser ist dessen Beschleunigung – d.h. desto schneller wird der Gegenstand schneller. Die physikalische Grösse für die Beschleunigung ist – wie auch jene für die Geschwindigkeit – stets mit einer Richtung versehen, die gemäss der Gleichung auch für die Kraft gilt.
Da die Corioliskraft mathematisch nur „in Erscheinung tritt“, wenn man das Fussballspiel wie der Astronaut von aussen beobachtet (die Zuschauer im Stadion in Oslo, die vor dem Abstoss mit Stadt und Ball um die Erdachse kreisen, kommen mit Hilfe der Vektoraddition weiter oben auf das Ziel des Balles), wird sie von den Physikern eine Scheinkraft genannt.
Die Corioliskraft ist aber durchaus real
Trotzdem könnt ihr selbst die Corioliskraft spüren, wenn ihr zum Beispiel versucht, auf einer sich drehenden Karussell-Scheibe auf dem Spielplatz geradewegs zu ihrem Mittelpunkt zu laufen. Das ist nämlich gar nicht so einfach – ihr müsst schon ordentlich gegenhalten, damit euch die Corioliskraft nicht von eurem direkten Weg ablenkt!
Ähnlich verhält es sich auch mit unserem unwahrscheinlichen Fussballspiel: Wenn die tunesische Küstenwache den Fussball aus dem Mittelmeer fischen und ins Stadion von Tunis bringt, sodass ein wiederum sehr starker Spieler den Ball in Richtung Oslo abstossen kann, würde auch er das Tor der Norweger nicht treffen. Denn da der Ball nun die höhere Drehgeschwindigkeit von Tunis mitnimmt, wird das langsamere Oslo den durch die Addition der Teilbewegungen ermittelten Zielpunkt beim Eintreffen des Balls noch nicht erreicht haben: Stattdessen fällt der Ball weiter östlich vielleicht auf die Grenze zwischen Norwegen und Schweden.
Die Regeln für die Ablenkung durch die Corioliskraft
Ganz gleich, in welche Richtung der Ball auf der Nordhalbkugel gespielt wird: In Flugrichtung gesehen lenkt die Corioliskraft den Ball stets „nach rechts“ (d.h. in Nord-Süd-Richtung nach Westen und in Süd-Nord-Richtung nach Osten).
Würde man ein ebenso unwahrscheinliches Fussballspiel auf der Südhalbkugel austragen, müsstet ihr die Zeichnung oben in einem Spiegel betrachten: An die Stelle des Nordpols tritt der Südpol (der ist auch auf jeder europäischen Landkarte unten, sodass ihr euren Atlas nun richtig herum halten könnt) und Osten ist nun rechts, sodass die Erde sich nun rechts herum dreht. Demnach „wirkt“ auch die Corioliskraft nun in spiegelverkehrter Richtung:
Ganz gleich, in welche Richtung der Ball auf der Südhalbkugel gespielt wird: In Flugrichtung gesehen lenkt die Corioliskraft den Ball stets „nach links“ (d.h. in Nord-Süd-Richtung nach Osten und in Süd-Nord-Richtung nach Westen).
Warum das unwahrscheinliche Fussballspiel?
Vielleicht habt ihr euch schon gefragt, weshalb ich so eine hanebüchene Begebenheit wie ein Fussballspiel von Oslo nach Tunis ersinne, um die Ablenkung durch die Corioliskraft zu beschreiben. Würden realistischere Umstände nicht den gleichen Zweck erfüllen?
Mit dieser klugen Frage kommen wir zu den Wasserwirbeln in Kenia und Tansania zurück. Der gekrümmte Pfeil in der Grafik deutet es schon an: Da die Ablenkung durch die Corioliskraft auf unterschiedlichen Geschwindigkeiten von Start- und Zielort einer Bewegung beruht, fällt eben diese Ablenkung um so grösser aus, je grösser der betreffende Geschwindigkeitsunterschied ist. Und der Geschwindigkeitsunterschied ist um so grösser, je weiter die Abstände von Start und Ziel von der Drehachse sich unterscheiden – d.h. je weiter Start und Ziel in Nord-Süd-Richtung voneinander entfernt liegen!
Warum die Corioliskraft für das Abfluss-Experiment keine Bedeutung hat
Beim Abfliessen aus einem vielleicht 40cm durchmessenden Trichter kommen die strömenden Wasserteilchen auf eine Bewegung von höchstens 20 Zentimeter in Nord-Süd-Richtung und wieder zurück. Dementsprechend winzig ist der Einfluss der Corioliskraft auf die Bewegungsrichtung der Teilchen – und dementsprechend einfach lässt sich die Bewegung durch andere Kräfte sehr gezielt beeinflussen.
Solche Kräfte lassen sich zum Beispiel durch eine angepasste Trichterform ausüben, welche die daran vorbei strömenden Wasserteilchen ganz unscheinbar in die gewünschte Richtung lenkt. Die Bemalung mit den auffälligen Spiralmustern lenkt recht erfolgreich von diesen kleinen Unterschieden ab.
Wenn ihr genau hinschaut, könnt ihr im Video erkennen, dass der Trichter, der „auf dem Äquator“ zum Einsatz kommt (welcher übrigens den Wirbel mittig halbiert, sodass die entgegengesetzte Wirkung der Coriolis-Ablenkung in der Nord- und Südhälfte sich aufheben soll), eine andere Form zu haben scheint als die Trichter für den Norden und den Süden.
Wo ihr die Auswirkung der Corioliskraft wirklich beobachten könnt
Wenn bei der Wettervorhersage im Fernsehen eine bewegte Wetterkarte zum Einsatz kommt, sind darauf meist riesige Wolkenwirbel zu sehen, die sich in die eine oder andere Richtung drehen. Es handelt sich dabei um Gebiete mit besonders hohem oder besonders tiefem Luftdruck. Ein hoher Luftdruck führt dazu, dass Luft in alle Richtungen von dem Gebiet wegströmt, während tiefer Luftdruck dazu führt, dass aus allen Richtungen zum betreffenden Gebiet hinströmt.
Diese Luftströmungen sind Hunderte bis Tausende Kilometer lang – und da die Lufthülle des Planeten sich im Grossen und Ganzen mit der Erde mitdreht, wirkt auf die strömenden Teilchen eine Corioliskraft. Die führt dazu, dass die Luftströme nicht geradlinig auf ein „Tief“ zu oder von einem „Hoch“ weg strömen, sondern in krummen, einen abflussähnlichen Wirbel bildenden Bahnen.
Der Coriolis-Ablenkung wegen drehen sich die Wirbel um Hochdruckgebiete auf der Nordhalbkugel stets „nach rechts“, also im Uhrzeigersinn, während die Wirbel um Tiefdruckgebiete – hier strömt die Luft in umgekehrter Weise – sich stets „nach links“, also gegen den Uhrzeigersinn drehen. Auf der Südhalbkugel, wo die Corioliskraft in seitenverkehrter Weise wirkt, ist das genau umgekehrt.
Um dagegen die Wirkung der Corioliskraft auf Wasserwirbel sichtbar zu machen, müssen diese mindestens ein paar Meter durchmessen und in aufwändig vor äusseren Einflüssen geschützter Umgebung im Labor kreisen können – auf der Strasse in Kenia funktioniert das jedenfalls nicht!
Seid ihr dem Mythos um die Drehrichtung von abfliessendem Wasser auch schon begegnet?
Und wenn ihr anlässlich der kommenden Weltmeisterschaft nur noch Fussball im Kopf habt, habe ich auch eine passende Anekdote aus der Chemie: Die Natur hat nämlich ein originalgetreues Fussball-Molekül erfunden!