Tag Archive for: Wasser

Belebtes Wasser – Gesundbrunnen oder wirkungsloses Fantasieprodukt?

, ,
Belebtes Wasser ist unwirksam - kein Gesundbrunnen, sondern Fantasieprodukt

Wenn ihr meine Kanäle verfolgt, habt ihr es wahrscheinlich schon mitbekommen: Ich schreibe an einem Mitmachbuch für Forscherkinder – über Wasser. Das ist schliesslich ein ganz besonderer Stoff und megaspannend. Da bleibt es nicht aus, dass Wasser allerorts, auch in den sozialen Medien, meine besondere Aufmerksamkeit weckt. So ist es mir unlängst in einer Kombination begegnet, die spontanes Chemiker-Augenrollen bewirkte: Als belebtes Wasser. Oder war es energetisiertes Wasser? Vitalisiertes Wasser? Aktiviertes Wasser? Magnetisiertes Wasser? Hexagonales Wasser? Oder sogar Grander-Wasser?

Merkt ihr was? So viele verschiedene und nichtssagende Begriffe für praktisch das gleiche. Und das ist nur eine Auswahl der Existierenden! Allein auf Psiram habe ich eine Liste mit 144 Firmen und Produktlinien rund um „verbessertes“ Wasser in vermutlich ebenso vielen Variationen gefunden! Also, worum geht es hier eigentlich? Um Wasser, das in irgendeiner Weise verbessert sein – und folglich positive Wirkungen auf uns haben soll.

Wie sollen wir an belebtes Wasser gelangen?

Die erwähnten Hersteller bieten entweder Gerätschaften und Anlagen zur „Verbesserung“ von Leitungswasser im eigenen Haushalt an oder sie verkaufen es fixfertig , zum Beispiel in Getränkeflaschen. Auffällig ist bei praktisch all diesen Produkten der hohe bis überrissene Preis.

Brauchen wir verbessertes bzw. belebtes Wasser?

Nein. In der Schweiz, Deutschland und Österreich geniessen wir das Privileg, einwandfreies Leitungswasser zu haben, das wir ohne Bedenken trinken können. In der Schweiz gilt das überdies für einen Grossteil der öffentlichen Brunnen.  Ausserdem können wir jederzeit ebenso einwandfreies Mineralwasser in Supermärkten kaufen. Und Leitungs- wie Mineralwasser bieten alles, was wir vom Wasser zum Gesundbleiben brauchen.

Was kann belebtes Wasser dann besser?

Ihr ahnt es sicher schon: Nichts. Zumindest nicht über einen Placeboeffekt hinaus. Und den könnt ihr wesentlich billiger haben.

Ist belebtes Wasser dann womöglich gefährlich?

Nicht direkt. Ausser für euren Geldbeutel. Denn Produkte rund um belebtes Wasser sind in der Regel mächtig teuer. Und bewirken, wie erwähnt, nichts.

Indirekt können sie aber zum Problem werden. Nämlich dann, wenn sie ein falsches Gefühl von Sicherheit vermitteln („das Wasser hält mich schon gesund“). Wenn aus diesem Sicherheitsgefühl heraus Arztbesuche verzögert, Medikamente nicht genommen oder andere wichtige Massnahmen vernachlässigt werden (Infektionsschutz ist zur Zeit ja ein ganz grosses Thema!), kann das schwerwiegende oder im schlimmsten Fall tödliche Folgen haben.

Aus diesem Anlass schreibe ich den Artikel: Nicht nur um eurer Geldbeutel willen, sondern vor allem, um euch dabei zu helfen, wirklich Gutes für die Gesundheit eurer Familie zu tun.

Um euch zu zeigen, warum belebtes Wasser nicht wirken kann, habe ich zunächst eine kleine Einführung in die Chemie des Wassers für euch.

Kleine Wasserkunde

1. Wasser ist eine Verbindung

Wasser ist einer von vielen Stoffen, aus denen unsere Welt aufgebaut ist. Dabei ist es zweifellos einer der wichtigsten Stoffe unserer Alltagswelt. Nahezu jeder von euch wird die chemische Formel, genauer die Summenformel, von Wasser schon einmal gesehen haben: H2O.

Diese Formel verrät uns schon eine ganze Menge über diesen Stoff. Sie sagt uns: Wasser besteht aus Molekülen. Ein Wassermolekül besteht wiederum aus zwei Wasserstoffatomen und einem Sauerstoffatom. Das bedeutet, Wasser ist kein Element, wie antike Philosophen annahmen, sondern eine chemische Verbindung. Ein chemisches Element besteht nämlich nur aus einer Sorte von Atomen – Wasser aber aus zwei Atomsorten.

2. Wassermoleküle sind gewinkelt

Die Atome in einem Molekül sind über Elektronenpaarbindungen miteinander verknüpft. Zwei Elektronen bilden eine solche Bindung. Die Regeln der Chemie besagen, dass ein Sauerstoffatom zwei Bindungen bilden kann und überdies noch zwei weitere, nichtbindende Elektronenpaare hat. Ein Wasserstoffatom kann dagegen nur eine Bindung bilden. Daraus ergibt sich die Strukturformel für Wasser:

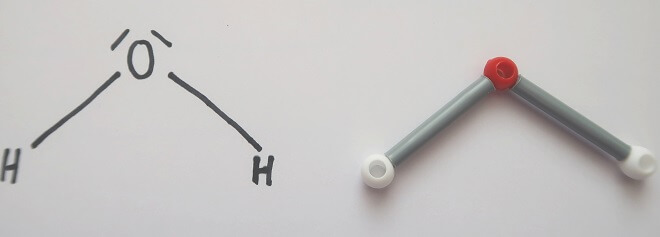
Wassermolekül: Lewisformel und Modell
Links: Strukturformel für Wasser, rechts ein Kugel-Stab-Modell des Wassermoleküls

Warum stehen die drei Atome nicht einfach in einer Reihe? Jedes Elektron trägt eine negative elektrische Ladung. Und gleiche elektrische Ladungen stossen einander ab. So gehen die vier äusseren Elektronenpaare – zwei Bindungen und zwei nichtbindende Paare – des Sauerstoffs auf grösstmöglichen Abstand zueinander. Und der entspricht annähernd der Nachbildung eines Tetraeders (einer regelmässigen dreieckigen Pyramide). Das Sauerstoffatom befindet sich im Zentrum dieser Pyramide, die beiden Wasserstoffatome und die Enden der nichtbindenden Elektronenpaare an den Ecken. Zeichnet man nun einen Längsschnitt, auf dem alle drei Atome liegen, durch das Gebilde, erhält man die gewinkelte Strukturformel des Wassermoleküls.

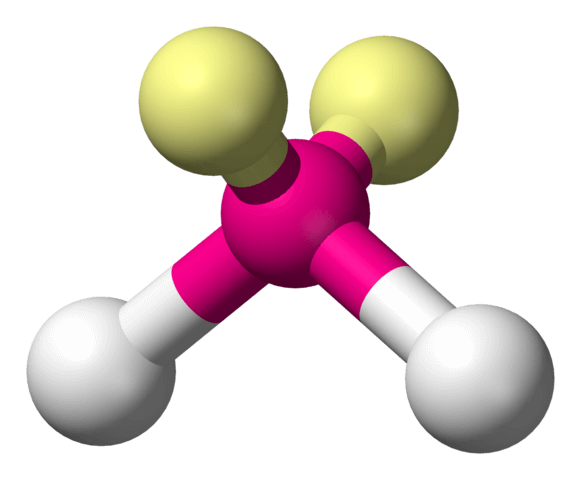
Wassermolekül mit nichtbindenden Elektronenpaaren - die Struktur erinnert an einen Tetraeder
Die gelben Kugeln stellen die nichtbindenden Elektronenpaare dieses Wassermoleküls dar. In dieser Anordnung sind die vier gelben und weissen Kugeln weitestmöglich voneinander entfernt!

3. Wassermoleküle sind elektrische Dipole

Nun verhält es sich so, dass Sauerstoffatome die Elektronen, auch jene in den Bindungen, viel stärker zu sich hinziehen als Wasserstoffatome. Deshalb ist in der Nähe des Sauerstoff-Atoms im Wassermolekül sehr viel mehr von den bindenden Elektronen anzutreffen als in der Nähe der Wasserstoffatome. Da jedes Elektron eine negative elektrische Ladung trägt, heisst das, dass am Sauerstoffatom mehr negative Ladung zu finden ist, als dort sein sollte, während an den Wasserstoffatomen zu wenig negative Ladung zu finden ist. „Mehr“ und „zu wenig“ stehen dabei für Ladungsmengen, die kleiner als die Gesamtladung eines Elektrons sind. 

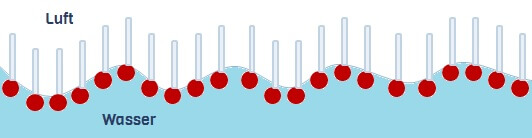
Nicht desto trotz bedeutet das, dass der Scheitel des Wassermoleküls (mit dem Sauerstoffatom) ein wenig negativ geladen ist, während sein „breites“ Ende mit den Wasserstoffatomen ein wenig positiv geladen ist (denn die positive Ladung der Atomkerne macht sich wegen des Elektronenmangels bemerkbar). Ein Wassermolekül hat also zwei elektrische Pole – deshalb nennt man es einen elektrischen Dipol.

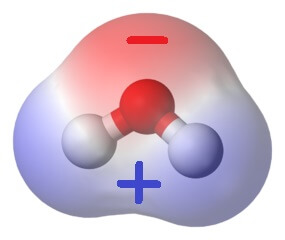
Wasserteilchen mit zwei Ladungs-Schwerpunkten
Ein Wassermolekül trägt zwei elektrische Ladungen: Die negative Seite (-) ist rot, die positive Seite (+) ist blau schattiert.

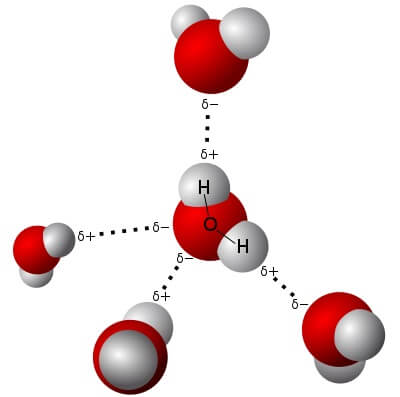
Verschiedene elektrische Ladungen aber ziehen einander an. So zieht der negativ geladene Scheitel eines Wassermoleküls unweigerlich die Breitseite seines nächsten Nachbarn an. Ebenso werden Wassermoleküle von anderen elektrischen Polen angezogen. Das könnt ihr mit diesem Experiment ganz leicht zu Hause zeigen!

Wasserteilchen: Entgegengesetzte Ladungen ziehen sich an.

4. Wasser ist sowohl eine Säure als auch eine Base

Die sehr „schiefe“ Verteilung der Elektronen im Wassermolekül führt aber nicht nur zu zwei elektrischen Polen, sondern auch dazu, dass die Bindungen zwischen Sauerstoff- und Wasserstoffatomen sehr brüchig sind. Ein Wassermolekül kann also sehr leicht einen Wasserstoffatomkern (ein H+-Ion) verlieren. Damit ist Wasser eine Säure. Ebensogut kann ein Sauerstoffatom eines seiner nichtbindenden Elektronenpaare verwenden, um solch ein verlorenes H+-Ion zu binden.  Damit ist Wasser eine Base.

Von einem Wassermolekül, das ein H+-Ion verloren hat, bleibt ein Hydroxid-Ion (OH–):

Ein Wassermolekül, das ein verlorenes H+-Ion aufnimmt, wird damit zum Hydronium-Ion (H3O+):

Tatsächlich kommt es ständig vor, dass ein Wassermolekül ein H+-Ion verliert, welches in einem anderen Wassermolekül Unterschlupf findet:

Ebenso kann das H3O+-Ion das zusätzliche H+-Ion wieder zurückgeben. So gibt es in einer Menge Wasser ein ständiges Herumgereiche von H+-Ionen zwischen den Wassermolekülen. Insgesamt findet man in einem Liter reinem Wasser zu jedem Zeitpunkt 0,0000001 mol oder 10-7 H3O+ – und ebenso viele OH– -Ionen. Der Exponent der Zahl der H+-Ionen (als Zehnerpotenz) in einem Liter Flüssigkeit mit umgekehrtem Vorzeichen ist nichts anderes als der pH-Wert. Reines Wasser hat also stets einen pH-Wert von 7.

5. Wassermoleküle können Wasserstoffbrücken bilden

Allerdings wäre das Ganze viel zu einfach, wenn man so strikt zwischen Bindung und keiner Bindung unterscheiden könnte. Das kann man nämlich nicht. Die Elektronen einer Bindung zwischen Sauerstoff- und Wasserstoff-Atom im Wassermolekül sind nämlich so ungleich verteilt, dass ein entblösster Wasserstoffkern sich in die dichte Elektronenhülle eines Sauerstoffatoms im Nachbarmolekül „einkuscheln“ kann, ohne sich dazu von „seinem“ Wassermolekül lösen zu müssen. Das nennen die Chemiker eine Wasserstoffbrücken-Bindung.

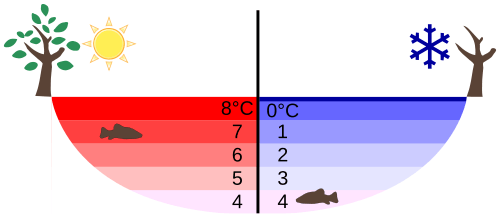
Das Resultat ist eine Anziehung zwischen Wassermolekülen, die noch stärker ist als die Anziehung zwischen ihren unterschiedlichen Ladungen (aber viel weniger stark als eine echte Elektronenpaarbindung). Sie zeigt sich zum Beispiel in dem enorm hohen Siedepunkt (100°C) von Wasser – da diese starke Anziehung überwunden werden muss, wenn das Wasser gasförmig werden will. Zum Vergleich: Der sehr eng verwandte Schwefelwasserstoff, H2S, der keine Wasserstoffbrücken bildet, siedet schon bei -60°C!

6. Wasserstoffbrücken entstehen zufällig und sind extrem kurzlebig

Die Darstellung von flüssigem Wasser als H2O ist somit im Grunde genommen eine Vereinfachung. Tatsächlich besteht flüssiges Wasser aus einem wilden Gemisch von Atomen, die sich mal als H2O, mal als H3O+ bzw. OH– gruppieren und sich noch viel öfter zu irgendetwas dazwischen zusammenkuscheln. Dabei kann es passieren, dass einige wenige Atome sich zu gut strukturierten Gruppen, sogenannten Clustern, zusammenrotten.

Aber dieser Austausch findet an jedem Ort im Wasser gleichzeitig und im Picosekundentakt statt. Das heisst, würde man ein Foto von den Bindungen zwischen Atomen in flüssigem Wasser machen, dann sähe ein zweites Bild davon, nur 0,000 000 000 001 Sekunden später aufgenommen, völlig anders aus – einschliesslich komplett anderer Molekül-Cluster.

Und das geschieht ganz spontan und zufällig. Die Triebkraft dafür ist zum Einen Wärmeenergie. Mit über 273°C über dem absoluten Nullpunkt (bei Atmosphärendruck) ist flüssiges Wasser nämlich immer ziemlich warm, auch wenn unsere Körper oft anderer Meinung sind. Und zum Anderen hilft das absolute Chaos, das der ständige Umbau mit sich bringt. Die Natur liebt nämlich Chaos – von Physikern und Chemikern „Entropie“ genannt – so sehr, dass sie ohne Energie von aussen ganz von selbst nach grösstmöglicher Unordnung strebt.

Warum man Wasser nicht beleben kann

Die meisten Anbieter in der „Belebtes-Wasser“-Branche behaupten, sie könnten flüssiges Wasser „besser“ machen, indem sie ihm irgendwie eine geordnetere Struktur geben. Einige fügen dem Wasser dafür Energie zu, andere berufen sich darauf, genau das nicht zu tun. Eines haben jedoch alle gemeinsam: Es kommt nichts dabei herum. Denn:

Wasser kann man nicht mit Energieeinsatz „beleben“, indem

  • Man man es über eine eingelegte Antenne mit elektromagnetischen Wellen berieselt. Würde man das mit Mikrowellen (der richtigen Frequenz bzw. Wellenlänge) machen, würde das Wasser allenfalls warm (so funktioniert ein Mikrowellenherd). Denn Mikrowellen der passenden Länge können elektrische Dipole wie Wassermoleküle in Drehung versetzen. Und die nehmen wir, wie jede andere ungerichtete Bewegung von Teilchen, als Wärme wahr. Infrarotwellen, die energiereicher als Mikrowellen sind, können ebenfalls wärmen – indem sie die Bindungen in Molekülen zum Schwingen bringen. Elektromagnetische Wellen mit weniger Energie bewirken hingegen nichts.
  • Man es mittels Elektrolyse ionisiert. Das mag zwar vorstellbar sein (wenn man vermeiden kann, dass statt irgendwelcher Ionen Moleküle von Wasserstoff- und Sauerstoff-Gas entstehen). Allerdings sorgt der stetige Austausch zwischen den Wasserteilchen dafür, dass sich nach dem Ausstellen der Elektrolysevorrichtung innert Picosekunden das oben erwähnte Gleichgewicht zwischen Wasser, H3O+– und OH–-Ionen wieder einstellt. Mit anderen Worten: So schnell, wie der pH-Wert von Wasser – sollte es ionisiert worden sein – wieder 7 ist, kann man es unmöglich trinken – geschweige denn anschauen.
  • Man es ebenfalls durch Elektrolyse mit Wasserstoff anreichert. „Wasserstoffwasser“ ist besonders in Japan als Fertigprodukt im Supermarkt beliebt. Grundsätzlich lässt sich Wasserstoff durch Elektrolyse von Wasser herstellen. Allerdings löst der sich nicht besonders gut in Wasser und kann in die allermeisten Festkörper (z.B Getränkeflaschen) problemlos ein- und durch sie hindurch wandern. So lässt sich Wasser nicht nur kaum mit Wasserstoff anreichern, sondern überdies auch kaum lagern. Dazu kommt, dass der menschliche Körper elementaren Wasserstoff (H2) gar nicht verwerten kann.
  • Man Wasser in ein (unveränderliches) Magnetfeld einbringt. Richtig ist: Elektrisch geladene Teilchen in Bewegung ändern im Magnetfeld ihre Bewegungsrichtung. Das gilt aber nur für Teilchen, die als Ganzes eine merkliche Ladung tragen. Wassermoleküle tragen zwar Ladungen, aber jedes von ihnen hat zwei gleich grosse, aber entgegengesetzte Ladungen, die einander aufheben. Von aussen gesehen bleibt so keine Ladung, auf die das Magnetfeld einen Einfluss haben könnte. Überdies ist Wasser ausschliesslich diamagnetisch und lässt sich daher nicht magnetisieren (Was hinter Dia-, Para- und Ferro-Magnetismus steckt erfahrt hier hier).
  • Man Edelsteine hineinlegt, die irgendwelche „Schwingungen“ oder „Informationen“ in das Wasser übertragen sollen. Die einzigen Schwingungen, die so übertragen werden können, sind jene Bewegungen, die wir als Wärme wahrnehmen. Würde man die Steine vorher erhitzen, könnte man so allenfalls das Wasser erwärmen (so funktionieren ein Tauchsieder oder der „heisse Stein“ im Restaurant).

Wasser kann man erst recht nicht ohne Energiezufuhr beleben, indem

  • Man in irgendeiner anderen Weise „Informationen“, „Schwingungen“ oder „Energie“ auf das Wasser überträgt (belebtes Wasser ‚im eigentlichen Sinn‘). Wie ihr in der kleinen Wasserkunde gelernt habt, hat flüssiges Wasser eine äusserst unstete Struktur: Seine Atome gruppieren sich in allerkürzesten Zeitabständen laufend neu. Das macht es zur Speicherung von Information für länger als 0,000 000 000 001 Sekunden vollkommen ungeeignet.

Kommt dazu – wie so oft – der ausdrückliche Verzicht auf Energie von aussen, gibt es zudem ein unlösbares Problem mit der Thermodynamik. Deren zweiter Hauptsatz besagt nämlich, dass die Schaffung von Ordnung in einem geschlossenen System ohne das Einbringen von Energie einfach nicht möglich ist. Und eine Struktur (z.B. in Form gespeicherter „Information“) in vormals chaotischem Wasser zu erzeugen, heisst Ordnung schaffen.

Das gilt gleichermassen für alle Spielarten belebten Wassers, ob sie nun belebtes Wasser, aktiviertes, vitalisiertes, levitiertes Wasser, „Grander-Wasser“ oder sonstwie heissen.

Aber der „Stand der Wissenschaft“ ist doch nicht unumstösslich?

Stimmt. Aber ein Grossteil dessen, was wir über Wasser wissen, ist so deutlich belegt, dass dort keine grossen Anpassungen des heutigen „Lehrbuchwissens“ mehr zu erwarten sind. Das gilt insbesondere für das unstete Betragen der Teilchen in flüssigem Wasser. Wir mögen zwar noch längst nicht alles über die erwähnten Wassercluster wissen. Doch das liegt eben gerade daran, dass diese Strukturen so kurzlebig sind, dass Wissenschaftler sie selbst mit hochtechnischen Apparaturen kaum vermessen können. Und ebendiese Kurzlebigkeit macht das Speichern von jedweder „Information“ in Wasser unmöglich.

Auch die Gesetze der Thermodynamik sind heute derart gut belegt, dass wir sie in unserer Welt getrost als unumstösslich annehmen können. Sollten Physiker dennoch jemals einen Weg finden, der am 2. Hauptsatz vorbei führt, dann nicht in der Welt, wie wir sie kennen, sondern unter höchst exotischen Bedingungen, die weit ausserhalb unserer persönlichen Reichweite liegen. Also nicht in unserem eigenen Keller oder einer mystischen Getränkefabrik.

Ausserdem haben sich die Wissenschaftler, die so gerne auf belastbare Studien pochen, sich nicht lumpen lassen. So gibt es auch Untersuchungen zur Wirksamkeit von belebtem Wasser auf Mensch, Tier und Pflanze – unabhängig von der Frage, ob sie mit heutigem Wissen theoretisch erklärbar wäre. Und hat man – unter belastbaren (also methodisch einwandfreien und wiederholbaren) Versuchsbedingungen – eine Wirkung gefunden? Nein.

Es gibt also weder eine nachweisliche Wirkung noch eine schlüssige Theorie, wie sie zustandekommen könnte. Mit anderen Worten: Belebtes Wasser ist demnach mit höchster Wahrscheinlichkeit ein reines Fantasieprodukt.

Wie ihr derartige Fantasieprodukte oder -angebote erkennen könnt

Einige auffällige Merkmale hat belebtes Wasser mit vielen anderen fragwürdigen Produkten und Angeboten im Gesundheitsbereich gemein: Es wird ihm eine so vielfältige Heilkraft nachgesagt, dass es leicht als Wundermittel durchgehen könnte.

  • Was gleichermassen gegen alles von Hauterkrankungen über Magenbeschwerden, Migräne, Depressionen u.v.a.m. bis hin zu Krebs hilft, kann nicht wirklich nützen. Verschiedene Krankheiten haben verschiedene Ursachen, die verschiedene Behandlungen erfordern. Darüber hinaus ist in der Schweiz und Deutschland die Werbung für Wasser mit Heilversprechen gesetztlich verboten, was eine solche um so unseriöser macht.
  • Ähnliches gilt für Angaben wie ‚hilft bei der „Entgiftung“ (Entschlackung,…). Die Notwendigkeit, Giftstoffe oder „Schlacken“ aus unserem Körper zu entfernen, ist ebenfalls ein Fantasieprodukt entsprechender Anbieter (denn das besorgen gesunde Leber und Nieren ganz allein).
  • Beliebte „Buzzwörter“ aus dem Alternativheilkunde-Bereich in Beschreibungen können ein Hinweis sein, dass dem Produkt das wissenschaftliche Fundament fehlt: Neben den genannten Synonymen für belebtes Wasser bzw. Wasserbelebung sind das z.B. „Schwingungen„, „Energien“ (Naturwissenschaftler verwenden „Energie“ nie in der Plural!), oder „feinstofflich„, die allesamt bedeutungslose Worthülsen sind. Dazu kommen die Namen Nicola Tesla, wenn es um mysteriöse Technik geht, oder – speziell im Wasserbereich – Gerald H. Pollack oder Masaru Emoto, auf deren nicht haltbare Theorien sich viele „Wasserbeleber“ beziehen, sowie Johann Grander.

Dazu kommen einige eigene Merkmale von Produkten rund um „verbessertes“ Wasser.

  • Das Verbot von Werbung für Wasser und Wasseraufbereitungsgeräte mit Heilversprechen in einem Grossteil des D-A-CH-Raums umgehen viele Anbieter, indem sie angebliche Wirkungen ihres Produkts nur über Kundenaussagen „kommunizieren“. Das geht über Kundenbewertungen und Testimonials oder Mund-zu-Mund-Propaganda. Hat euch „nur“ jemand von einem tollen Gerät/Produkt/Angebot erzählt? Findet ihr Aussagen zu gesundheitlichen Wirkungen nur von anderen Kunden und nicht vom Hersteller selbst? Dann ist Vorsicht angesagt!
  • Wirkungslose Anlagen und Geräte zur „Verbesserung“ von Wasser wie auch fixfertig belebtes Wasser werden häufig zu horrenden Preisen angeboten. Wenn ihr ein fragwürdiges Angebot unter die Lupe nehmen möchtet, vergleicht es einmal mit ähnlichen Produkten ohne „Esoterik“-Label. Fixfertig belebtes Wasser also mit Mineralwasser, als besonders wirksam oder geeignet deklarierte Edelsteine mit den gleichen Steinen ohne solche Attribute beim Mineralienhändler, Elektrokleingeräte mit Haushaltsgeräten aus ähnlichen Bestandteilen, Geräte zum Einbau ins Eigenheim mit „herkömmlichen“ Wasserfiltern für die Trinkwasserzuleitung. Beträgt der Unterschied ein Vielfaches, ist da in der Regel etwas faul.

Wenn euch ein Angebot mit solchen Merkmalen über den Weg läuft, verzichtet guten Gewissens darauf. Dann könnt ihr das Geld für andere Dinge einsetzen, die wirklich gesundheitsfördernd sind: Für einen schönen Familienurlaub zum Beispiel, Mitgliedschaften im Sportverein, Musikstunden, oder einfach für abwechslungsreiches Essen.

Und wenn es dazu schon zu spät ist?

Ihr habt bereits eine Anlage zur Wasserbelebung im Keller? Oder ist der bereits in ein Lager für fixfertig belebtes Wasser umgewandelt?

Zunächst einmal: Ihr seid damit nicht allein. Selbst Betreiber von Schwimmbädern, Spitäler oder eine österreichische Gewerkschaft haben sich schon von solchen Angeboten ködern lassen und eine Menge Geld verbraten. Die können nämlich – ganz offensichtlich – ziemlich verlockend sein und auf den ersten Blick sehr seriös wirken. Bloss zeigt das nicht, wie nützlich die Produkte sind, sondern die Geschäftstüchtigkeit ihrer Anbieter. Und die mag nicht zuletzt daher rühren, dass die Hersteller und Vertreiber selbst an die Wirksamkeit ihrer Produkte glauben (zumindest konnten selbst Anwälte vor Gericht ihnen bislang nichts Gegenteiliges nachweisen).

Besonders wenn Mund-zu-Mund-Propaganda ins Spiel kommt – im schlimmsten Fall innerhalb einer eingeschworenen Community rund um Hersteller und Produkt oder im eigenen Freundeskreis – kann der Einfluss bzw. Druck von „aussen“ auf eure Entscheidungen immens werden. Und wer will es sich schon mit der besten Freundin oder dem netten Forum verscherzen, weil er ein ja soo nützliches Ding kategorisch ablehnt?

Wirksames von Fantasieprodukten zu unterscheiden ist manchmal schwierig

Dazu kommt, dass viele Produkte, Angebote und auch Literatur so seriös und „medizinisch“ aussehen, dass es für Laien echt schwierig sein kann, wirklich Sinnvolles von Fantasieprodukten zu unterscheiden.

Selbst ich als Chemikerin habe einmal mit grossem Interesse in einem populärwissenschaftlichen Buch von Gerald H. Pollack gelesen. Das fiel mir in der Stadtbibliothek auf der Suche nach Literatur über Wasser in die Hände. Das las sich spannend und erst einmal schlüssig – davon abgesehen, dass ich von den dargestellten Theorien und Phänomenen weder in der Schule noch im Studium gehört hatte. Doch was wäre ich für eine Chemikerin, würde ich, ein paar Jahre aus dem Uniumfeld draussen, neue Forschungsergebnisse von vorneherein als unmöglich abstempeln? So fühlte ich mich selbst mit Chemie-Diplom nicht in der Lage, das Buch aus dem Stand sicher einzuordnen. Dabei haben mir erst weitere Recherchen geholfen.

Was tun, wenn das Geld weg ist?

Ist das belebte Wasser erst einmal im Haus und das Geld weg, wenn eure Zweifel überhand nehmen, verbucht das Ganze am besten als Gelegenheit zum Lernen. Wie mein Vater immer sagt: Geld ist den grossen Kummer nicht wert. Und ein Grund, sich zu schämen oder hämische Bemerkungen anhören zu müssen, ist das Ganze meines achtens auch nicht (dahingehend können Anhänger der Skeptiker-Szene im Umgang mit Anhängern solcher Fantasien oft noch eine Menge lernen).

Wichtig ist: Selbstreflexion

Stattdessen fragt euch, was euch wirklich dazu gebracht hat, euch auf belebtes Wasser einzulassen und allenfalls viel Geld dafür auszugeben? Hattet ihr wirklich ein eigenes Bedürfnis danach (z.B. um eine Krankheit zu lindern)? Da belebtes Wasser nachweislich nicht wirkt: Überlegt euch – was fehlt euch wirklich (oder hat gefehlt)? Welche andere(n) Massnahme(n) könnte(n) für eine scheinbare Wirkung des Wassers verantwortlich sein?

Oder habt ihr euch unter dem Einfluss anderer entschieden – Familie, Freunde, (Online-)Community? Wie könnt ihr euch solchen Einflüssen künftig entziehen? Und was bedeuten euch die betreffenden Personen oder Gruppen wirklich? Denn im schlimmsten Fall, wenn ein Druck sich nicht abwehren lässt, kann eine Trennung von ihnen der beste Ausweg sein.

Was ihr in jedem Fall tun könnt

Ob ihr nun selbst in die Falle hineingetappt seid oder nicht, ihr könnt eure Mitmenschen davor bewahren, auf solche sinnlosen Angebote einzugehen.

Dabei erachte ich dies als ganz besonders wichtig:

Nehmt euer Gegenüber ernst. Hinter der Entwicklung unsinniger Glaubensvorstellungen stecken praktisch immer Bedürfnisse oder Ängste, die befriedigt oder gelöst werden wollen, und oft ein erheblicher Einfluss eines äusseren Umfelds (Familie, Freundeskreis, Onlinecommunity,…), der eben diese Bedürfnisse bedient.

Ermuntert eure Mitmenschen, diese Bedürfnisse zu ergründen und sich die unter „Selbstreflexion“ vorgeschlagenen Fragen zu stellen.

Verkneift euch, wenn ihr euch zu den „Skeptikern“ zählt, hämische Bemerkungen oder Bezeichnungen. Zeigt den Betroffenen stattdessen, dass ihr sie als Menschen wertschätzt und gebt ihnen so einen Anreiz, die vermeintliche Zuflucht fragwürdiger Glaubenssätze oder Umfelder zu verlassen.

Und tut das vor allem von Anfang an. Denn je früher Anhänger von Glaubenssätzen, wie jenen um belebtes Wasser, Alternativen zu ihren „Alternativen“ aufgezeigt bekommen, desto höher ist die Chance, sie noch zu erreichen.

Auch wichtig ist: Weitere Verbreitung verhindern

Erinnert euch daran, wie diese fragwürdigen Produkte verbreitet werden. Nämlich über Mund-zu-Mund-Propaganda.

Wenn ihr eure Mitmenschen davor bewahren wollt, auf den Hype um belebtes Wasser (oder andere Fantasie-Produkte) hereinzufallen, dann hört, falls ihr das je getan habt, in jedem Fall auf, sie weiter zu verbreiten und schön zu reden. Oder fangt erst gar nicht damit an. Entfernt oder ändert allfällige positive Bewertungen im Internet, sofern ihr das selbst könnt (Testimonials, die Firmen selbst auf ihren Seiten einfügen, werden diese kaum wieder löschen).

Denn was andere auch behaupten: Belebtes Wasser wirkt nicht über einen Placeboeffekt hinaus.

Besonders lobenswert ist natürlich, wenn ihr euch aktiv für die Aufklärung rund um belebtes Wasser und Co. einsetzt. Erst recht, wenn ihr eine Entscheidungsposition bezüglich der Weiterverbreitung fragwürdiger (und nicht fragwürdiger) Angebote innehabt – sei es auf eurer eigenen Website, in den „grossen“ Medien, einschliesslich Magazinen von Krankenversichereren, Grossverteilern und anderen Branchen, oder gar in der Politik.

Dazu könnt ihr gerne diesen Artikel weiterverbreiten und findet weiteres Material in den Links darin. Zum Beispiel diesen Artikel, in dem Dr. Erich Eder, ein grosser Kritiker des „Grander-Wassers“, beschreibt, wie ihr eure Kritik so formulieren könnt, dass ihr möglichst kein juristisches Vorgehen der Anbieter belebten Wassers riskiert (und wie ihr damit umgehen könnt, falls es doch dazu kommt).

Scheut euch dabei nicht, euren eigenen Fehlentscheid einzugestehen, falls euch einer unterlaufen ist. Hört oder lest darüber hinweg, solltet ihr anfangs abfällige Bemerkungen und Kommentare kassieren. Und trennt euch rigoros von jenen, die sie nicht lassen können. Denn (nicht nur) in meinen Augen zeugt es von wahrer Grösse, seine Ansicht aufgrund neuer Erkenntnisse zu ändern und das auch kundzutun. Und letztendlich kann ein „ich habe das selbst durch, ich weiss, wovon ich rede“ eure Position nur stärken.

Seid ihr belebtem oder sonstwie „verbessertem“ Wasser auch schon begegnet? Wie geht ihr mit Leuten um, die darauf schwören oder/und zu seiner Verbreitung beitragen?

/2 Comments/by

Experiment: Eis schneiden – oder auch nicht

,
Experiment für Kinder: Eis schneiden

Kann man einen Eiswürfel zerschneiden? Sicherlich…oder doch nicht? In diesem Experiment könnt ihr durch Eis schneiden, ohne es dabei zu zerteilen. Klingt nach Zauberei? In jedem Fall aber nach der wahrlich zauberhaften Physik von Wasser!

Ein Eiswürfel- Experiment für kalte coole Tage

Mit dem letzten Wochenende kamen die ersten kalten Tage des bevorstehenden Winters. Das ist genau die richtige Zeit für buchstäblich „coole“ Experimente mit Eis und Wasser. Bei beiden handelt es sich natürlich um den gleichen Stoff – einmal fest, einmal flüssig. Und bestimmt wisst ihr auch, bei welcher Temperatur das Wasser am der Erdoberfläche diesen Zustand ändert. Richtig: Bei 0°C schmilzt Eis bzw. gefriert flüssiges Wasser.

Das ist an sich nichts besonderes. Die meisten Stoffe wechseln an der Erdoberfläche bei einer bestimmten Temperatur vom festen zum flüssigen Zustand und zurück. Nur manche Stoffe wie Kohlenstoffdioxid oder Jod werden ohne Umweg vom Feststoff zum Gas (Physiker sagen, diese Stoffe „sublimieren“, anstatt zu schmelzen).

Wasser hat darüber hinaus jedoch eine weitere Eigenschaft, dank derer ihr es für geradezu magische Phänomene und Experimente gut ist. Und ein solches Experiment für Kinder möchte ich euch heute vorstellen: So könnt ihr durch Eis schneiden ohne es zu zerteilen – und dabei nicht nur die Anomalie des Wassers nutzen, sondern auch lernen, wie Schlittschuhe funktionieren.

Ihr braucht dazu

  • Eiswürfel
  • eine Gabel
  • 1,5l-Getränkeflasche mit Inhalt oder ähnliches Gewicht (leichtere gehen auch, aber: je schwerer das Gewicht, desto besser!)
  • dünnen Draht
  • einen Tisch
  • Klebeband (Panzertape hält sehr gut und lässt sich erstaunlich einfach wieder ablösen)
  • einen grossen Behälter (Wanne, Backblech,…)

So geht’s

  • Klebt den Stiel der Gabel so auf dem Tisch fest, dass das Kopfstück mit den Zinken über den Rand der Tischplatte schaut.
Der Gabelstiel ist mit Panzertape an der Tischplatte festgeklebt. So trägt er das 1,5kg - Gewicht locker!
Mit Panzertape hält die Gabel bombenfest und lässt sich nach dem Experiment doch gut wieder lösen.
  • Platziert das grosse Gefäss unter der überhängenden Gabel. Der Boden soll schliesslich nicht nass werden, wenn euer Eiswürfel schmilzt.
  • Wickelt ein Stück Draht so um den Hals der gefüllten (ob mit Wasser oder sonst einem Getränk ist egal) Flasche, dass eine lange Schlaufe absteht.
  • Nehmt einen Eiswürfel aus dem Gefrierfach und legt ihn auf die Zinken der Gabel.
    Hängt die Drahtschlaufe über den Eiswürfel und lasst die daran hängende Flasche vorsichtig los.
  • Wartet einige Minuten ab und beobachtet!
Gabel, Eiswürfel und Wasserflaschen-Gewicht mit Auffangblech am Tisch
Aufbau im Ganzen: Oben an der Tischkante die Gabel mit dem Eiswürfel, darüber der Draht, an welchem die Flasche hängt. Das Backblech unten fängt Schmelzwasser auf – so bleibt der Parkettboden heil.
Im Hintergrund ein Blick hinter die Kulissen: Das Fotozelt – hier Lichtquelle – liefert bei den handlicheren Experimenten in Keinsteins Kiste den weissen Hintergrund!

Was ihr beobachten könnt

Der Draht sinkt langsam nach unten in das Eis. Dabei entsteht jedoch kein Spalt. Stattdessen verfestigt sich das Eis über dem  Draht erneut! Wenn der Eiswürfel nicht zu schnell schmilzt, schneidet sich der Draht den ganzen Weg hindurch – ohne das Eis zu zerteilen!

Sicht von vorne: Der Draht ist vollständig in den Eiswürfel eingesunken.
Nach einigen Minuten ist der Draht komplett in den Eiswürfel eingesunken!

Tipp: Je kühler die Umgebungsluft, desto weniger schnell schmilzt der Eiswürfel weg. Wenn es im  Zimmer zu warm ist, könnt ihr das Experiment ebenso gut im Garten oder auf dem Balkon machen. Je nachdem, wo ihr das Experiment aufbaut, braucht ihr dann auch kein Auffanggefäss für das Schmelzwasser.

Eiswürfel frei schwebend auf der Drahtschlaufe: Runterfallen ist unmöglich!
Der Beweis: Hier halte ich nur die Flasche fest! Der Eiswürfel ist wie eine Perle auf dem Draht „aufgefädelt“ und schwebt somit abseits der Gabel frei.

Was passiert da?

Um Eis zu schmelzen ist Energie nötig (das könnt ihr mit diesem Experiment deutlich machen). Wenn man einen Stoff schmelzen möchte, führt man diese Energie normalerweise in Form von Wärme zu. Wasser – und das macht diesen Stoff so einzigartig – kann allerdings auch durch Druck zum Schmelzen gebracht werden.

Die Gewichtskraft, die auf die Flasche wirkt (und einer Masse von mindestens 1,5kg bei Erdanziehung auf Bodenhöhe entspricht), zieht den Draht nach unten. So übt er an der Auflagefläche Druck auf das Eis aus und lässt es unter dem Draht schmelzen.

Wie kann Druck zum Schmelzen von Eiskristallen führen?

Wasser ist ein ganz besonderer Stoff. Während die Dichte (die Masse eines bestimmten Volumens) der meisten Stoffe um so grösser wird, je kälter die Stoffe werden, hat Wasser bei +4°C die grösste Dichte.

Das heisst, ein Kilogramm Wasser bei 4°C braucht nicht nur weniger Platz als ein Kilogramm Wasser bei 20°C, sondern auch weniger als ein Eisblock von einem Kilogramm Gewicht (der höchstens 0°C warm sein kann). Dass Eis „grösser“ ist als flüssiges Wasser, könnt ihr übrigens mit diesem Experiment zeigen: Eis wächst!

Wirkt ein Druck auf einen Stoff, wird dieser – wenig überraschend – zusammengedrückt. Die meisten Stoffe brauchen unter hohem Druck als Feststoffe am wenigsten Platz. Da Wasser jedoch als Flüssigkeit am „kleinsten“ ist, wird es unter Druck flüssig – und das erst noch, ohne besonders warm zu werden. Denn denn wenigsten Platz braucht es ja bei nur 4°C oberhalb seines Schmelzpunktes.

Die Moleküle von flüssigem Wasser sind – anders als im Eiskristall – weitestgehend frei beweglich. So gelangen sie um den Draht herum, der somit nach unten auf das verbleibende Eis sinkt und es weiter schmelzen kann. Auf diese Weise „schneidet“ sich der Draht durch den Eiswürfel.

Warum friert der Spalt über dem Draht wieder zu?

Sobald das flüssige Wasser einen Weg um den dünnen Draht herum gefunden hat, steht es kaummehr unter Druck (der Atmosphärendruck ist natürlich noch vorhanden, spielt hier aber keine massgebliche Rolle). So kann es sich wieder auf seine ursprüngliche Grösse ausdehnen. Da zum Ausdehnen Energie aufgewendet werden muss, kühlt die unmittelbare Umgebung dabei ab, und das Wasser oberhalb des Drahtes wird wieder zu festem Eis.

Schlittschuhspass dank der Anomalie des Wassers

Diese besondere Fähigkeit des Wassers habt ihr wahrscheinlich schon genutzt, ohne es zu wissen. Auf diese Weise funktionieren nämlich Schlittschuhe: Die Kufen üben Druck auf das Eis aus, sodass dessen Oberfläche direkt unter ihnen schmilzt. So entsteht ein dünner Film aus beweglichen Wassermolekülen, auf welchem eure Schlittschuhe fast ohne Reibungswiderstand über das Eis gleiten können!

Dabei müsst ihr euch keine Sorgen machen, dass eure Eisfläche durch das Schlittschuhlaufen wegschmilzt. Denn sobald eure Kufen weiter geglitten sind, kann sich das darunter zusammengedrückte Wasser wieder ausdehnen und gefrieren. Wenn ihr das nächste Mal auf der Eisbahn seid, achtet darauf: So lange die Lufttemperatur nicht übermässig hoch ist, werdet ihr keine flüssigen, sondern allenfalls fest wirkende Spuren hinterlassen.


Entsorgung

Wenn ihr die Eiswürfel aus Leitungswasser gemacht habt, könnt ihr das Schmelzwasser nachher wie Leitungswasser verwenden: In den Ausguss geben, die Blumen damit giessen,… Den Inhalt der Getränkeflasche könnt ihr selbstverständlich trinken – und damit zum Beispiel auf den gelungenen Versuch anstossen ;).

Sollte das Klebeband Rückstände auf dem Tisch hinterlassen, können Lösungsmittel wie Brennsprit/Spiritus (Ethanol), Fleckbenzin oder Aceton bei der Entfernung helfen. Testet vorher immer, ob eure Tischoberfläche sich mit dem Lösungsmittel eurer Wahl verträgt! Mein Panzertape habe ich übrigens ganz ohne Rückstände von der matt lackierten Holzplatte lösen können.

Nun wünsche ich euch viel Spass beim Experimentieren! Erzählt doch mal, wie das Experiment bei euch funktioniert – oder von euren Beobachtungen beim Schlittschuhlaufen!

Hast du das Experiment nachgemacht: 

[poll id=“6″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/0 Comments/by

Experiment: Blätter transportieren Wasser – ein Kontrollversuch macht es sichtbar!

Experiment: Blätter transportieren Wasser - und warum ein Kontrollversuch wichtig ist

Es ist Herbst, und langsam färben sich die Blätter bunt. Sie zu sammeln und aufzuheben macht Freude. Aber wenn man nicht achtgibt, rollen sie sich nur zu schnell ein und werden spröde. Aber warum werden lose Blätter trocken? Weil sie nichts mehr zu trinken haben, ist eine naheliegende Antwort. Aber nicht die einzige: Dazu kommt, dass Blätter ständig Wasser an die Luft abgeben – als Wasserdampf, der von ihrer Oberfläche verdunstet.

Dieses Experiment zeigt, wo Pflanzen das Wasser hernehmen – und dass sie es tatsächlich von einem Ort an einen anderen befördern können.

Ihr braucht dazu

  • 2 gleiche Gläser
  • Wasser
  • einen Zweig mit grünen Blättern
  • etwas Speiseöl
  • ggfs. Pasteurpipette (z.B. Deckel einer Nasentropfen-Flasche)
Links: Glas mit einem Blatt einer Glyzine („Blauregen“), Rechts: Kontrolle ohne Blatt
Ich habe Olivenöl verwendet, dass eine gelbliche Farbe hat. Andere Speiseöle sind weniger farbig, funktionieren aber ebenso.
Bei dem dünnen Blattstiel hätte ich aber ewig warten können…

So geht’s

Füllt die Gläser etwa zwei Drittel hoch mit Wasser. Die Füllhöhe soll dabei in beiden Gläsern gleich sein. Schneidet den Zweig am unteren Ende schräg an und stellt ihn in ein Glas. Bedeckt nun die ganze Wasseroberfläche in beiden Gläsern mit einer Schicht Speiseöl. Eine Pipette kann beim sauberen Dosieren helfen. Ausserdem könnt ihr mit der Pipettenspitze das Öl zum Glasrand hin verstreichen, bis es daran kleben bleibt. Stellt anschliessend beide Gläser für einige Stunden, besser einen Tag lang an die Sonne oder in einen warmen Raum.

Mit einem verholzten Zweig vom Kirschbaum samt sieben Blättern konnte ich schliesslich doch einen Effekt beobachten…

Was ihr beobachten könnt

Der Wasserspiegel im Glas mit dem Zweig sinkt mit der Zeit, während jener im Glas ohne Zweig unverändert bleibt.

Nach zwei bis drei Stunden an der Sonne steht das Wasser im Glas mit den Zweigen 1 bis 2 Millimeter weniger hoch als im Kontrollglas.
Nach einem zusätzlichen Tag im Innenraum fällt das Ergebnis noch deutlicher aus: Der Unterschied beträgt jetzt mehr als 5 Millimeter!

Was passiert da?

Blätter geben über kleine Poren (Spaltöffnungen) an ihrer Oberfläche ständig Wasser(-dampf) an die Luft ab.

Blätter unter dem Mikroskop, mit sichtbaren Spaltöffnungen
Dies ist die untere Aussenhaut eines frischen Blattes meiner Tomatenpflanze bei 100-facher Vergrösserung. Die winzigen Spaltöffnungen (sie sind ca. 0,05 – 0,1 mm klein!) sind als dunkelgrüne Punkte gut erkennen (die Ränder der Spalten enthalten den grünen Blattfarbstoff Chlorophyll, die übrigen Aussenhautzellen nicht). Diagonal durch das Bild verläuft eine „Blattader“, d.h. Leitungsbündel, in dessen Umgebung ebenfalls chlorophyllhaltige Zellen haften geblieben sind.

Durch den Wasserverlust entsteht ein Unterdruck, der über die Wurzeln der Pflanze Wasser aus dem Boden nach oben saugt. Als Leitungen dienen dabei dünne Röhren im Inneren der Stängel sowie die „Adern“ in den Blättern. Da der geschnittene Zweig weder Wurzeln noch Boden hat, wird das Wasser im Experiment direkt aus dem Glas gezogen. Mit dem Stängel werden nämlich auch die Röhren darin angeschnitten, sodass sie nun offen ins Wasser ragen. Mit dem schrägen Schnitt vermeidet ihr, dass die Öffnungen der Röhren flach auf den Glasboden gedrückt und so verschlossen werden.

Warum rollen sich trockene Blätter nun ein?

Einen guten Teil des in die Blätter hinauf gesogenen Wassers gibt die Pflanze nicht sofort wieder ab. Stattdessen speichert sie es in kleinen Hohlräumen (Vakuolen) in ihren Zellen. Sind die Vakuolen prall gefüllt, sind auch die Zellen prall und das Blatt erscheint straff und fest.

Wenn der Wassernachschub ausbleibt, werden die Vakuolen zunehmend entleert: Die Blätter werden zunächst schlaff (dieser Teil lässt sich umkehren und die Pflanze „wiederbeleben“ – wie genau, erfahrt ihr hier). Wenn die Wasservorräte ganz verbraucht sind, können die Blattzellen nicht mehr funktionieren und sterben ab. Ohne pralle, formgebende Wasserspeicher fallen die „Skelette“ der sterbenden und toten Zellen regelrecht in sich zusammen, sodass das Blattgewebe krumm und spröde wird.

Und wozu das Speiseöl?

Das Speiseöl verhindert, dass Wasser über die Wasseroberfläche verdunstet. So muss das Wasser, das im Glas mit dem Zweig fehlt, von dessen Blättern „ausgeschwitzt“ worden sein!


Ein Forschertrick: Sichere Ergebnisse durch Kontrollversuche

Das zweite, leere Glas dient als direkte Vergleichsmöglichkeit: Ihr könnt den Unterschied zwischen einem Glas mit Verdunstungsmöglichkeit über einen Zweig und einem Glas, aus dem nichts verdunsten kann, auf einen Blick sehen. So könnt ihr

  1. auch kleine Unterschiede rasch erkennen.
  2. sicher gehen, dass ihr den Zweig auch dann „schwitzen“ seht, wenn doch etwas Wasser durch das Öl verdunsten sollte. Das geschähe dann nämlich in beiden Gläsern in gleicher Weise. Folglich muss ein sichtbarer Unterschied etwas mit dem Zweig zu tun haben.

Auch die grossen Forscher machen Kontrollversuche

In der wissenschaftlichen Forschung sind solche Kontrollversuche von entscheidender Wichtigkeit. Je komplizierter die Versuche nämlich sind, desto mehr Umstände können das Ergebnis beeinflussen. Besonders wenn Lebewesen an Experimenten beteiligt sind, sind Forscher oft gar nicht in der Lage, jeden einzelnen dieser Umstände nachzuvollziehen und seinen Einfluss auf das Ergebnis zu bestimmen.

Ein Kontrollversuch unter möglichst gleichen Bedingungen, aber ohne das Detail, das man untersuchen möchte, zeigt einem die Summe aller zusätzlichen Einflüsse. Wenn das zu untersuchende Detail zu einem davon unterschiedlichen Ergebnis führt, kann man sicher sein, dass eben dieses Detail auch die Ursache dafür ist. Und das, ohne jeden einzelnen Umstand mit Einfluss zu kennen!

Das gilt für einfache Experimente wie den Nachweis eines Stoffs mit einem Reagenz bis hin zu Studien, in welchen Medikamente an Menschen getestet werden.

Mit Kontrollversuchen lässt sich der Placebo-Effekt „ausblenden“

Bei solchen Studien erhält eine zusätzliche Gruppe von Versuchspersonen, die „Kontrollgruppe“ genannt wird, ein Medikament ohne Wirkstoff – ein sogenanntes Placebo. Das menschliche Gehirn ist nämlich ein besonders schwer zu kontrollierender Einfluss auf Versuchsergebnisse: Es lässt uns selbst dann eine Veränderung unseres Befindens wahrnehmen, wenn kein Wirkstoff im genommenen Medikament ist (das nennen die Forscher den Placebo-Effekt)!

Der Placebo-Effekt tritt (wie viele andere Umstände) sowohl bei der Kontrollgruppe als auch bei der Gruppe mit Wirkstoff auf. Wenn das Ergebnis bei der Gruppe mit Wirkstoff trotzdem anders ist als das bei der Kontrollgruppe, hat das mit ziemlicher Sicherheit der Wirkstoff bewirkt. Gibt es dagegen keinen Unterschied zwischen der Gruppe mit Wirkstoff und der Kontrollgruppe, bewirkt der „Wirkstoff“ ebenso sicher nichts.   


Zusammenfassung

Dieses einfache Experiment zeigt, dass Pflanzen Wasser aus dem Boden (oder einem Glas) „trinken“ und als Wasserdampf an die Luft abgeben können.

Ein Kontrollversuch ohne Pflanze macht diesen Effekt im Vergleich direkt sichtbar. Ausserdem lässt sich mit seiner Hilfe ausschliessen, dass andere Faktoren für das Verschwinden des Wassers aus dem Glas verantwortlich sind. Derartige Kontrollen sind ein äusserst wichtiger Bestandteil wissenschaftlicher Forschung.

Ihr könnt euch die Trink- und Schwitz-Fähigkeit von Pflanzen übrigens direkt zu Nutze machen: Zimmerpflanzen im Raum sorgen dafür, dass auch im Winter die Raumluft nicht zu trocken wird!

Entsorgung

Den Zweig könnt ihr auf den Kompost oder in den Grünabfall geben. Oder ihr lasst ihn als Dekoration im Wasserglas stehen oder verwendet ihn für weitere Blatt-Experimente.

Wasser und Speiseöl könnt ihr in den Ausguss entsorgen. Die Super-Waschkraft von Spülseife hilft dabei, Ölreste von den Gläsern zu entfernen und fort zu spülen. Nicht verwendetes Speiseöl könnt ihr natürlich zum Kochen weiterverwenden.

Oder ihr nehmt bloss den Zweig aus dem Glas und verwendet es samt Inhalt für das Experiment mit der DIY-Lavalampe!

Ich wünsche euch viel Spass beim Experimentieren!

Hast du das Experiment nachgemacht:

[poll id=“7″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/0 Comments/by

Experiment mit Wasser : Die Münzenwippe

Experiment mit Wasser : Die Münzwippe

Endlich hat es gewittert und ein wenig abgekühlt! Dazu war heute vormittag noch Regen angesagt. Zeit für ein kleines Experiment für zwischendurch, das ihr sowohl draussen als auch drinnen machen könnt. Dabei geht es um die Superkräfte von Wasser ….oder doch nicht?

Unglaubliche Kräfte schlummern nämlich nicht nur in Wasser, sondern auch in der Luft! – Und diese Kräfte könnt ihr mit ganz einfachen Mitteln selbst erforschen:

Ihr braucht dazu

  • ein Trinkglas
  • einen glatten Pappstreifen, aus einem Tetrapack zugeschnitten
  • kleine Münzen (z.B. Fünfräppler, aber Eurocents tun es genauso)
  • Wasser
Für das Experiment braucht ihr: Trinkglas, Wasser, Pappstreifen aus Tetrapak, kleine Münzen

Die Idee habe ich von „Schule und Familie„. Wie dort beschrieben mit einem einfachen Pappstreifen funktioniert das Experiment aber nicht so recht: Die Pappe saugt sich im Nu mit Wasser voll, wird weich und krumm, sodass die Münzen vorzeitig abrutschen. Die „Innen-„seite eines Tetrapacks ist jedoch wasserdicht beschichtet (das Getränk soll ja im Karton bleiben). Da wird nichts krumm und die Münzwippe funktioniert wunderbar.

So geht’s

  • Füllt das Glas randvoll – und ein Bisschen darüber hinaus – mit Wasser. Das Wasser soll sich leicht über den Glasrand aufwölben. Eine saubere Tropfpipette (zum Beispiel der Deckel einer Nasentropfen-Flasche, gibt es auch einzeln für kleines Geld in der Drogerie!) kann dabei helfen, die letzten Tropfen vorsichtig einzufüllen.
  • Legt den Tetra-Pappstreifen mit der „Innenseite“ nach unten und mit einem Ende so auf das Glas, dass er die Öffnung ganz verschliesst. Vielleicht merkt ihr schon, wie er sich festsaugt.
Alles bereit: Ein Ende der Pappe liegt mit der Beschichtung nach unten auf dem Glas.
Alles bereit: So liegt die Pappe richtig auf dem Glas!
  • Stapelt nun vorsichtig eine Münze nach der anderen auf das überhängende Ende. Der Streifen wird trotz Übergewicht eine ganze Weile auf dem Glas liegen bleiben! Ich habe fünf Fünfräppler geschafft, bevor der Streifen sich beim sechsten schliesslich doch gelöst hat. Wer schafft mehr?
Die Münzwippe in Aktion: Das Gewicht von fünf Fünfräpplern kann den Pappstreifen nicht vom Glas lösen!
Fünf „Füüferli“ und es hält immernoch…

Was passiert da?

Superkraft von Wasser : Adhäsion

Das zunehmende Gewicht der Münzen auf dem überhängenden Ende lässt den Pappstreifen wie auf dem Glas festgeklebt erscheinen. Wie festgeklebt? Dabei handelt es sich bei Weitem nicht nur um einen Vergleich!

Wassermoleküle werden tatsächlich von vielen anderen Stoffen angezogen und ziehen selbst wiederum diese Stoffe an. Diese Erscheinung nennen die Physiker „Adhäsion“ – und die anziehenden Kräfte „Adhäsionskräfte“. Es gibt verschiedene Theorien, wie diese Adhäsionskräfte zustande kommen. Aber die meisten davon haben gemeinsam, dass die Teilchen von Stoffen sich genau dann besonders anziehend finden, wenn bestimmte ihrer Eigenschaften sich ähneln.

Eine dieser Eigenschaften ist die Ausstattung von Teilchen mit elektrischer Ladung. Wenn ihr schon einmal den Zaubertrick mit dem krummen Wasserstrahl ausprobiert habt, wisst ihr, dass Wassermoleküle relativ starke Ladungen tragen (für die etwas fortgeschritteneren Forscher unter euch: Physiker nennen Wasser deshalb „polar“). So ziehen sie nicht nur einander stark an, sondern werden auch von anderen Stoffen mit elektrischen Ladungen angezogen.

Gemäss dieser „Polarisationstheorie“ wäre also davon auszugehen, dass auch die Innenfläche des Getränkekartons elektrische Ladungen trägt bzw. polare Bestandteile hat, die Wassermoleküle anziehen und so zum Haftenbleiben bringen.

Aber eigentlich ist es doch gar nicht wünschenswert, dass das Getränk im Tetrapack kleben bleibt! Deshalb werden die Tetrapack-Entwickler doch sicher vermieden haben, ein all zu adhäsionsfreudiges Material für ihre Beschichtung zu verwenden. Und trotzdem klappt das Experiment…

Superkraft von Luft : Luftdruck

Eine zweite Erklärung für den „klebenden“ Pappstreifen ist, dass die Pappe weniger am Wasser klebt, als dass sie durch die Luft darauf gedrückt wird. Die Erdatmosphäre, die aus unzähligen frei umherwuselnden Teilchen besteht, drückt nämlich von allen Seiten auf jedes Hindernis, das ihr in die Quere kommt.

Die wuselnden Teilchen trommeln laufend auf jede von Luft umgebene Oberfläche ein – und wir nehmen dieses Dauer-Trommelfeuer mit unseren groben Sinnen als Druck wahr. Der Luftdruck am Erdboden beträgt etwa 1 bar (oder 1000 Millibar), was eine beträchtliche Menge ist. Schliesslich drückt ja eine gut 30 Kilometer hohe Luftsäule auf die wuselnden Teilchen in eurer Nähe und drängt sie so eng zusammen, dass sie entsprechend dicht und heftig auf alle Oberflächen trommeln.

So auch auf den Pappstreifen, der auf dem Glas liegt. Dieser Luftdruck ist so stark, dass er – allenfalls gemeinsam mit einer ziehenden Adhäsionskraft – die Münzen auf dem freien Streifenende aufwiegt: Der Luftdruck (und die Adhäsion) drücken das Glasende des Pappstreifens zunächst stärker nach unten als das Gewicht der Münzen das freie Ende. Erst wenn das Gewicht der Münzen zu gross wird, wippt das freie Ende des Streifens nach unten, während das Glas-Ende nach oben schnellt.

Da diese „Wippe“ nicht am Angelpunkt auf dem Glasrand befestigt ist, fällt der Aufbau damit sofort zusammen.

Münzwippe überlastet: Der Pappstreifen ist vom Glasrand gekippt.
…aber die sechste Münze war zu viel: Der Streifen wippt in Richtung der Münzen und stürzt vom Glasrand.

Bonus-Versuch für draussen

Ihr wollt sehen, wie stark der Luftdruck sein kann? Dann füllt wie oben beschrieben das Glas bis zum Rand mit Wasser und legt den Pappstreifen darauf, sodass die Öffnung vollständig bedeckt ist. Haltet den Streifen fest und dreht das Glas mit der Öffnung nach unten. Dann lasst den Pappstreifen los (das Glas natürlich nicht!). Wenn alles gutgeht, sorgt der Luftdruck allein dafür, dass die Pappe auf der Öffnung und das Wasser im Glas bleibt!

Weil dieses Experiment aber nicht immer auf Anhieb funktioniert empfehle ich euch dringend, das draussen oder im Badezimmer zu probieren! Da richtet eine mögliche Überschwemmung nämlich keinen grossen Schaden an.

Entsorgung

Die ist bei diesem Versuch denkbar einfach:

Da ich mit Trinkwasser aus der Leitung und ausschliesslich mit Hilfsmitteln aus der Küche experimentiert habe, trinke ich das Wasser gerade aus, während ich blogge 😉 . Auch sonst könnt ihr das Wasser noch für alles benutzen, wozu man Wasser braucht. Den Tetra-Pappstreifen könnt ihr aufheben, sodass ihr die Experimente jederzeit wieder vorführen und eure Lieblingsmenschen verblüffen könnt.

Nun wünsche ich euch viel Spass beim Experimentieren! Und…kennt ihr vielleicht Gelegenheiten aus eurem Alltag, bei welchen ihr (wirkliche) Adhäsionskräfte beobachten könnt?

Hast du das Experiment nachgemacht: 

[poll id=“8″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/0 Comments/by

Rätsel-Experiment für Gross und Klein: Womit funktioniert der Eiswürfel-Kran?

Rätsel-Experiment für Kinder: Womit funktioniert der Eiswürfel-Kran?

Wenn es draussen kalt und grau ist, mache ich es mir gerne im Warmen gemütlich. Aber was tun an langen Tagen daheim? Ich habe für euch ein winterliches Rate-Experiment:

Mit welcher „magischen“ Substanz könnt ihr einen Eiswürfel an einem Bindfaden befestigen und hochheben?

Nein, ich meine nicht Klebstoff. Der würde an einem Eiswürfel soundso nicht haften, sondern ratzfatz wieder abgehen, wenn das Eis schmilzt. Es gibt jedoch einen anderen Stoff, der den Bindfaden dank eines raffinierten physiko-chemischen Tricks ganz wunderbar am Eiswürfel haften lässt.

Lasst die Kinder den „magischen“ Stoff erraten!

Welcher Stoff kann sowas? Lasst insbesondere eure Nachwuchs-Forscher darüber nachdenken (und ratet selbst mit, wenn ihr noch nicht darauf gekommen seid), bevor ihr weiter (vor-)lest. Dann könnt ihr nach folgender Anleitung ganz einfach selbst ausprobieren, ob ihr recht hattet.


Experiment: Wir bauen einen Eiswürfel-Kran


Ihr braucht dazu

  • einen Eiswürfel
  • ein Glas Wasser
  • einen stabilen Holzstab(Schaschlikspiess etc.)
  • ein Stück Bindfaden
  • Zucker oder Salz oder Pfeffer oder Kaugummi
Das braucht ihr: Glas mit Wasser, Holzspiesse, Bindfaden, Eiswürfel

Nur mit einem dieser Stoffe funktioniert das Experiment. Nennt den Nachwuchs-Forschern ruhig diese Vier zur Auswahl. Vielleicht kommen sie selbst darauf, was sie wirklich brauchen. Stattdessen könnt ihr auch alle vier Möglichkeiten ausprobieren.

So geht’s

  • bindet das Stück Bindfaden an euren Stab, sodass ein kleiner Kran entsteht
  • legt den Eiswürfel in das Wasserglas: Er schwimmt (Wieso? s. hier–>Eis wächst)
  • fragt spätestens jetzt die Nachwuchs-Forscher: Was glaubt ihr: Welche der genannten Zutaten ist geeignet, um den Eiswürfel an den Faden zu heften?
  • streut etwas von der „magischen“ Substanz auf den Eiswürfel und legt das freie Ende des Fadens dazu.
  • wartet ca. 30 Sekunden
  • hebt den Eiswürfel vorsichtig am Faden aus dem Wasser.

Das könnt ihr beobachten

Wenn ihr die richtige Zutat gefunden habt, haftet der Eiswürfel am Faden, sodass ihr ihn aus dem Wasser heben könnt!

Der Eiswürfel hängt frei am Bindfaden!
Geht nur mit der richtigen Zutat: Der Eiswürfel hängt frei am Bindfaden!

Welches ist die richtige „magische“ Substanz?

Erinnert ihr euch an die Wirkweise von Streusalz (die habe ich hier erklärt)? Wenn dessen Ionen sich mit Wasser mischen, bringt das Eis in der Umgebung zum Schmelzen. Die Wassermoleküle sind nämlich derart damit beschäftigt, die Salzionen zu umhüllen, dass sie nicht mehr am stetigen Schmelzen und Gefrieren, das sich zwischen Eis und Wasser abspielt, teilhaben können.

Und dann – so besagt es das Gesetz von Le Châtelier – müssen diese Wassermoleküle ersetzt werden. Indem mehr Eis zu flüssigem Wasser schmilzt, als es das normalerweise tut.

Das Schmelzen aber verbraucht Energie, entzieht der Umgebung also Wärme. Die Umgebung von Salz und Faden kühlt also ab, bis schliesslich selbst das Salzwasser mitsamt dem Faden am Eiswürfel festfriert!

Entsorgung

Sobald das Eis geschmolzen ist, könnt ihr das Salzwasser einfach in den Abfluss geben. Zum Blumengiessen eignet es sich wahrscheinlich nicht mehr, da die Pflanzen zu viel Salz nicht vertragen.

Alltagstipp: Eis und Salzwasser als Kühlmittel

Im Labor nutzen Chemiker die Abkühlung, die Salz in Eiswasser verursacht, zur Kühlung von Experimenten, bei denen zu viel Wärme frei wird. Streusalz ist ein billiges Mittel dafür. Das entstehende Salzwasser ist zudem nicht giftig, sodass es nachher einfach in den Abfluss entsorgt werden kann.

Tafelsalz ist zwar etwas teurer, funktioniert aber ebenso: Wenn eure Getränke im Eiswürfelbad einmal nicht kalt genug werden, gebt etwas Wasser und Salz dazu und rührt vorsichtig, um ein Eisbad zwischen 0°C und -10°C zu erhalten!

Und probiert ihr den Eiswürfelkran selbst aus? Über eure Erfahrungsberichte freue ich mich sehr!

Hast du das Experiment nachgemacht: 

[poll id=“13″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/0 Comments/by

[Werbung] Ausflugstipp: Abenteuer Umweltschutz im Sea Life Center Konstanz

Ausflugstipp: Sea Life Center Konstanz - mit Gewinnspiel

Reto und ich haben vom Sea Life Center Konstanz für die Begehung vor Ort kostenfreien Eintritt und eine Zusage für den Versand weiterer Freikarten für eine Familie plus Plüsch-Schildkröte als Souvenir für die Kinder als Gewinn erhalten. Ich bedanke mich sehr für die Zusammenarbeit! Es besteht kein Interessenkonflikt hinsichtlich des Inhalts in diesem Beitrag und dessen Publikation.

Was ist Sea Life?

Bestimmt habt ihr schon mal von „Sea Life“ gehört. Schliesslich steht dieser Name für die grösste Besucher-Aquarienkette der Welt. In 47 Städten rund um die Welt (32 davon in Europa) gibt es ein Sea Life Center, in welchem kleinen und grossen Besuchern die Bewohner von Meeren, Flüssen, Seen und anderen Gewässern in aufwändig gestalteten Aquarien ganz nahe gebracht werden.

Die Sea Life Center werden von der Merlin Entertainment Group betrieben, dem grössten Anbieter von Unterhaltungseinrichtungen und Freizeitparks in Europa und dem zweitgrössten solchen Unternehmen weltweit. So gehören neben den Sea Life Aquarien zum Beispiel auch die Legoland-Freizeitparks und die „Madame Tussaud’s“-Wachsfiguren-Kabinette (die man längst nicht mehr nur in London findet) zum Konzern.

Wie kommt nun Unterhaltungsindustrie in Keinsteins Kiste?

Die Sea Life Center möchten mehr als bloss unterhalten. Sie möchten informieren, eine geheimnisvolle und gefährdete Welt erlebbar machen und so kleinen und grossen Besuchern nahe bringen, wie wichtig es ist, die Gewässer der Erde und ihre Bewohner zu schützen.

So haben Sea Life und ich etwas gemeinsam: Wir möchten euch spannende Geheimnisse der Natur und ihre Erforschung näher bringen. Um euch zu zeigen, wie viel Spass Natur und Wissenschaft machen können, aber auch um Grundlagen für verantwortungsvolles Tun in allen Lebenslagen schaffen. Denn was Menschen kennen und schätzen, werden sie auch respektieren und schützen.

Heute darf ich euch auf Einladung des Sea Life Centers in Konstanz eine Entdeckungsreise durch die Unterwasserwelt vorstellen, im Rahmen derer ihr euch selbst als Meeresforscher versuchen könnt. Und das Beste daran: Das Sea Life Center hat seine Einladung auf euch erweitert: Ich darf Eintrittskarten für eure ganze Familie in das Sea Life Aquarium in Konstanz verlosen! Wie das vor sich geht, erfahrt ihr am Ende dieses Beitrags.

Jetzt geht es aber los auf Tauchgang

Reto und ich haben uns einen regnerischen Samstag Anfang September für unseren Besuch im Sea Life Konstanz ausgesucht. Das trübe Wetter scheint perfekt dafür, um „indoor“ in fremde Welten abzutauchen. Die Sommerferien in Baden-Würtemberg und Bayern sind allerdings noch nicht zu Ende. So müssen wir damit rechnen, dass wir längst nicht die einzigen sind, die heute hier auf Tauchgang gehen.

So laufen wir bereits auf der mächtigen Rampe zum Eingang des Sea Life Centers auf eine Warteschlange auf. Die allerdings könnte grösser sein – es finden sogar alle Wartenden unter dem Vordach im Trockenen Platz. Direkt am Bodensee, am Konstanzer Hafen gelegen wirkt das Gebäude von aussen eher schlicht, ist durch den markanten Schriftzug an der Fassade aber unverkennbar.

Sea Life Center Konstanz - Aussenansicht

Freundlicher Empfang

Dank der freundlichen und fleissigen Mitarbeiter an der Kasse erreichen wir nach einigen Minuten den Eingangsbereich, der schon erahnen lässt, wie das Innere dieses Grossaquariums geschnitten ist: Eng und lauschig.

Deshalb meine Empfehlung an Familien mit kleinen Kindern: Vor dem Eingang gibt es einen überdachten Kinderwagen-Parkplatz. Nutzt den und lasst Kinderwagen und allfällige andere Fahrzeuge unbedingt draussen! Ihr tut euch selbst und allen anderen Gästen damit einen grossen Gefallen!

An der Tageskasse erhalten wir unsere Freikarten und ein Informationsblatt mit den Schau-Fütterungszeiten. Am Samstag werden allerdings nur die Pinguine gefüttert (die Fische in den anderen Becken brauchen nicht jeden Tag etwas zu fressen, lernen wir später), sodass wir diesen Fixpunkt gleich auf unsere gedankliche Agenda setzen.

Für unsere Kinder könnten wir jetzt Material für zusätzliche interaktive Stationen und Forscher-Aufgaben in der Ausstellung zubuchen. Unser Hauptaugenmerk liegt heute aber auf dem neuesten Angebot hier in Konstanz, das im Eintrittspreis enthalten ist: Wir dürfen uns selbst am Traumberuf „Meeresforscher“ versuchen und eine in Not geratene Meeresschildkröte retten.

 

Im Sea Life durch die Welt der Gewässer und Meere

Das Sea Life Konstanz zeigt die Wasserbewohner entlang einer Reise den Rhein hinunter, durch den Bodensee und weiter bis nach Rotterdam, von dort ins offene Meer, in tropische Ozeane, den Amazonas hinauf und schliesslich an den Rand der Antarktis am fernen Südpol der Erde.

So beginnt unser Tauchgang in einer künstlichen Gletscherhöhle, wie sie in den Höhen der Alpen an der Quelle des Rheins zu finden sein mag. Ein Willkommensvideo soll vornehmlich die kleinen Besucher in grundlegende Hausregeln und den Gebrauch der Zusatzmaterialien einführen. Eine automatisch öffnende Tür am Ende des Raumes, die die Besucher für den Rundgang dosieren soll, sorgt für ein gewisses Freizeitpark-Gefühl. Da wir aber im Aquarium sind, zieht es die meisten Besucher, die die Tür von Hand aufschieben, gleich weiter. Wir lassen uns ebenfalls vom Strom treiben.

Umweltschutz für Kinder aufbereitet

Unser Weg führt durch aufwändig ausgestaltete Räume an den Bewohnern des Rheins und des Bodensees in offenen Becken vorbei. Kindgerechte und humorvolle Beschreibungstafeln und -bildschirme geben den gezeigten Tieren Namen – sind aber weniger ausführlich als die klassischen Gehege-Tafeln im Zoo. Das bedeutet zwar weniger Informationen für die Grossen, ermöglicht jedoch auch weniger lesesicheren Primarschulkindern, die Ausstellung selbstständig zu entdecken.

Dabei wird stets grosses Gewicht auf den Natur- und Umweltschutz gelegt: Es werden in jedem Bereich Projekte vorgestellt, mit welchen sich der Sea Life Trust für den Schutz der Wasserbewohner und ihrer Lebensräume engagiert. Ausserdem werden Tipps gegeben, wie wir alle dazu beitragen können, indem wir unseren Lebenswandel auf den Schutz von Meeren und Gewässer ausrichten können.

Für die Kleinsten gibt es zudem reichlich Hocker, die auf den Weg durch die Ausstellung mitgenommen werden können und – vor allem später – den Blick in etwas höher gelagerte Becken ermöglichen.

Im Raum mit dem Bodensee-Becken fällt mir dann erstmals die Hintergrund-Musik auf, die uns durch die ganze Ausstellung begleitet. Dezent gibt sie der Unterwasser-Erlebniswelt einen kinowürdigen Soundtrack.

 

Unser Hauptziel: Die interaktive Schildkröten-Rettung

Gleich hinter Konstanz am Bodensee finden wir uns – einem Unterbruch der Reiseroute gleich – am interaktiven Schildkrötenstrand wieder. In diesem Raum ist mächtig etwas los, möchten sich doch alle Kinder einmal als Meeresschützer versuchen. Und es gibt hier reichlich zu tun:

Hier am "Strand" gibt es viele Schildkröten zu retten!

Am „Strand“ haben wir auch am regnerischen Feriensamstag reichlich Auswahl an Plüsch-Schildkröten in Not. Ich entscheide mich für ein Exemplar und trage es gleich zur Waage. Ein Mikrochip im Innern des Plüschtiers kommuniziert mit dieser Station. Auf dem Bildschirm können wir die Art auswählen, der unsere Schildkröte angehört, und ihr einen Namen geben. Unser Schützling soll „Keinstein“ heissen. Die Waage teilt uns ausserdem mit: Keinstein, die Unechte Karettschildkröte, wiegt viel zu wenig. Er muss dringend aufgepäppelt werden!

Plüsch-Schildkröte "Keinstein" auf der Waage

Meine Wahl fiel auf „Keinstein“, die unechte Karettschildkröte.

 

Technik mit Kinderkrankheiten…

So geht es weiter zur Schildkrötentränke. Hier zeigt sich eine Kinderkrankheit der empfindlichen Technik: Die Fortschritts-Daten in Keinsteins Chip werden nicht erkannt: Der Bildschirm schickt uns zurück zur Waage. Eine aufmerksame und sehr hilfsbereite Sea Life-Mitarbeiterin bietet uns gleich eine Ersatz-Schildkröte an. Wir geben jedoch nicht so schnell kleinbei – wir wollen schliesslich Keinstein retten. Also noch einmal zurück auf Anfang.

Und dann klappt alles reibungslos.

Keinstein hat sich satt gefressen!

Alles richtig gemerkt – und Keinstein ist satt!

An der Fütterungsstation zeige ich, dass ich mir gut gemerkt habe, was Unechte Karettschildkröten am liebsten fressen. An der Röntgenstation werde ich selbst zur Tierärztin, denn Keinstein ist ganz schön ramponiert: Pflaster, Verband und Salbe sorgen dafür, dass alle Blessuren rasch heilen können.

Keinstein in der Röntgenkammer: Floss gebrochen!

Oh weh, Flosse gebrochen! Da hilft wohl nur ein Pflaster…oder doch ein stabiler Gipsverband?

Bis es soweit ist, gibt es endlich etwas zu trinken. Wir messen die gewünschte Menge Wasser ab und pumpen sie durch die abenteuerliche Installation gleich in Keinsteins Maul.

Keinsteins hat Durst!

Keinstein hat Durst! Nur noch abmessen, dann gibt es was zu trinken.

Dann heisst es Abschied nehmen: Das Display zeigt an, dass wir alle Meeresschützer-Aufgaben erfolgreich erledigt haben. Keinstein ist gesund und munter und darf ins Meer zurück. Also setzen wir ihn am „Strand“ aus und sehen ihm nach, während er wieder ins Meer zurück kriecht – um bald aufs neue von einem Kind gerettet zu werden.

Wir setzen Keinstein am "Strand" wieder aus.

Tschüss, Keinstein! Auf dass noch viele Kinder dich retten mögen!

 

… ist dank hervorragender Betreuung kein Problem

Die moderne Technik ist scheinbar noch recht empfindlich und mit „Kinderkrankheiten“ behaftet. Dank der sorgfältigen Betreuung durch die Mitarbeiter „strandet“ aber niemand bei diesem Abenteuer. Ein Bisschen Geduld zahlt sich dabei wie so oft aus: Im zweiten Anlauf klappt alles prima.

Und das obwohl die Anlage recht störanfällig zu sein scheint. Zum Glück ist jede Station in vierfacher Ausführung eingerichtet. So stört selbst an diesem betriebsamen Samstag kaum, dass ein bis zwei Ausgaben je Station gerade defekt sind.

Alles in allem ist die Schildkrötenrettung besonders für Jungforscher ein herziger wie lehrreicher Spass für zwischendurch, bevor es weiter auf die Reise durch die Meere geht.

 

Meeresbewohner zum Staunen

Besondere Freude macht mir in Einrichtungen wie dem Sea Life, die jungen Besucher zu beobachten und ihnen zuzuhören.

Zum Beispiel dem kleinen Jungen, der mit grossen Augen in das (für meine recht verwöhnten Erwachsenensinne nur mässig spektakuläre) Quallenbecken schaut: „Mama, sind das auch Tiere?“ (Ja, antwortet die Mutter.) „Wo (bzw. wie) fühlen die sich wohl?“

Ohrenqualle im Aquarium

Ja, das ist auch ein Tier: Die Ohrenqualle – eine völlig harmlose Bewohnerin der Ostsee

Oder den beiden Mädchen am Rotterdamer Hafenbecken: „Papa, da ist ein langer Fisch! Was ist das für einer?“ (Sie müssen etwas warten, bis sie Papas Aufmerksamkeit auf die rechte vordere Ecke des Beckens lenken können, bleiben aber hartnäckig.) „Ein Aal“, erklärt der Vater. „Ist das ein Zitteraal?“

Ist er nicht – es handelt sich um den europäischen Aal. Rund 30 Jahre älter als diese Kinder verbinde ich diesen Aal noch mit einem geräucherten Leckerbissen auf der Weihnachtstafel. Heute sind die Bestände so überfischt, dass der Räucheraal rar geworden ist. So rar, dass diese Kinder ihn nicht mehr kennen. Um so wichtiger ist es, ihnen solche Tiere nahe zu bringen.

Tierwelt für alle Sinne

In der kleinen Halle mit dem grossen, offenen Rochenbecken finden wir ein weiteres kleines Highlight: Am Berührbecken dürfen wir und die mutigen Jungforscher die bizarrren Eihüllen der Rochen und Haie in die Hand nehmen und uns von durchsichtigen Garnelen anknabbern lassen. Einige Seesterne und andere Tiere in weiteren Becken machen gerade Berühr-Pause. Animateurin Melanie, die wir bereits von der Pinguinfütterung kennen, hat ein wachsames Auge und spannende Erklärungen dazu parat.

Physik-Tricks im Aquarium

Der Übergang in wirklich tropische Gefilde beginnt mir einer weiteren rar gewordenen Gattung: Den Seepferdchen. Eine besonders grosse und eindrückliche Art wird hier sogar nachgezüchtet! Auf weniger augenscheinliche Expemplare gewähren nach aussen gewölbte Halbkugel-Becken einen besonders guten Blick. Die gläserne Wölbung hat nämlich die gleiche Wirkung wie eine Lupe: Sie bricht das Licht auf eine Weise, die das Innere des Aquariums grösser aussehen lässt, als es wirklich ist!

Seepferdchen im hinter kugelrundem Glas

Seepferdchen vergrössert: Die Glas-Halbkugel wirkt wie eine Lupe!

Dahingegen wirken nach innen gewölbte Glasscheiben wie ein Weitwinkelobjektiv: Das Innere des Aquariums wirkt zwar kleiner, aber wir haben da hindurch einen besonders grossen Teil des weitläufigen Beckens im Blick.

„Findet Nemo“ im tropischen Meer

Im tropischen Meer gelangen wir schliesslich zu der Art Becken, für das die Sea Life-Center bekannt sind: Ein Plexiglas-Tunnel, durch den wir „unter Wasser“ hindurchgehen – und einen Hai von unten in Augenschein nehmen – können. Besonders spannend an der Konstanzer Ausführung ist, dass wir dieses Becken während des Rundgangs aus verschiedenen Richtungen einsehen und immer neues entdecken können.

Reto mit Fotomodell im Plexiglastunnel

„Fische sind Freunde – und Reto auch“, denkt sich wohl dieser Hai, der auf der Tunnelwölbung posiert.

So erwische ich nicht nur Reto beim Foto-Shooting mit einem besonders bequemen Hai, sondern auch einen sehr lebendigen Kollegen von unserem „Keinstein“. Und wer besonders aufmerksam ist, findet in diesem und den umliegenden Becken praktisch alle wichtigen Charaktere aus „Findet Nemo“, dem Animationsfilm um den kleinen Clownfisch aus dem Indischen Ozean.

Wer findet Nemo im Korallenbecken?

Wer findet Nemo im Korallenbecken?

 

Spektakel im Süsswasser: Tropischer Regenwald

Auch im Tropenwald gibt es viel Wasser – das berühmteste Gewässer ist wohl der Amazonas-Fluss. Diesem ist der vorletzte Ausstellungsraum gewidmet. Zwei besonders populäre Bewohner sind hier vertreten: Eine Art der vielfältigen giftigen Pfeilgiftfrösche und die berüchtigten Piranhas. Letztere lösten vor allem deshalb Staunen aus, weil sie sich fernab ihrer Fütterungszeit (nur Montags um 15 Uhr) in ihrem schillernden Schuppenkleid ausnehmend schön präsentierten.

Doch auch weniger bekannte und um so spektakulärere Arten wie Diskusfische finden hier Platz.

Ein Diskusfisch im Amazonas-Becken

Diskusfische wie dieser spucken Wasser, um Insekten über der Wasseroberfläche „abzuschiessen“ und nach dem Absturz in den Fluss zu fressen.

 

Fütterung bei den Eselspinguinen

Unsere Tauchfahrt führt uns zu guter Letzt in die eisige Antarktis – genauer gesagt an deren erfrischend kühlen Rand. Dort – genauer gesagt auf den Falkland-Inseln – leben nämlich die im Sea Life Konstanz präsentierten Eselspinguine.

In den meisten Zoos und Aquarien, die ich kenne, werden die ebenfalls in milderem Klima heimischen Humboldt-Pinguine gehalten. So sind die zehn Vögel hier für Reto und mich eine willkommene Abwechslung – und sehen im Übrigen der Schweizer Fernseh-Knetfigur „Pingu“ richtig ähnlich.

Der Eselspinguin betrachtet uns Besucher genauso neugierig wie wir ihn.

Wer ist hier nun im Zoo? Irgendwie fühlen wir uns beobachtet…

Um die Fütterung nicht zu verpassen, sind wir zwischenzeitlich von unserem Rundgang fort ans Ende der Ausstellung geeilt und haben uns zur lebhaften Besucherschar in den recht begrenzten Raum geschoben. So kommt es, dass uns Melanie, die Moderatorin, später am Berührbecken schon bekannt ist.

Hier erklärt Melanie kindgerecht spannend und humorvoll, warum wir nicht mit Blitz fotografieren, an die Scheiben klopfen oder durch das Glas mit den Tieren spielen sollen (die Pinguine stossen sich dabei den Schnabel und können sich so verletzen). Während ein Tierpfleger die Vögel hinter dem Glas mit Fisch versorgt, erzählt unsere Moderatorin Wissenswertes zu den Pinguinen. So lernen selbst wir noch etwas neues:

Warum gibt es schwule Pinguine?

Das Sea Life Konstanz hat einst fünf Pinguin-Pärchen, also fünf Männchen und fünf Weibchen anschaffen wollen. Wie sich bald zeigte, sind jedoch sechs der erhaltenen Tiere männlich und vier weiblich. So gibt es nun vier Pärchen, die Nachwuchs bekommen können – und zwei Männchen bilden ein schwules Paar. Aber warum macht die Natur sowas?

In der freien Natur muss stets ein Elternteil das gemeinsame Ei auf den Füssen hüten, während der andere Elternteil auf Nahrrungssuche geht. Später werden dann die Rollen getauscht. Wenn nun der jagende Elternteil von einer Robbe oder einem anderen Feind gefressen wird und nicht zurückkehrt, muss der andere Elternteil irgendwann das Ei allein zurücklassen, um nicht zu verhungern. Schwule (oder lesbische) Pinguin-Paare adoptieren solche verwaisten Eier und ziehen gemeinsam das Junge gross. So können die homosexuellen Vögel zur Erhaltung ihrer Art beitragen, obwohl sie keinen eigenen Nachwuchs zeugen.

 

Der Tauchgang ist fast ein wenig zu schnell vorbei

Als wir das Pinguinbecken abseits der Fütterungszeit ein zweites Mal erreichen, finden wir auch die angekündigten Unterschriftenbögen von Greenpeace zur Unterstützung des Antarctic Trust, der sich für die Erhaltung von Arten und Lebensräumen rund um den Südpol einsetzt. Von den Eindrücken unserer Unterwasser-Reise beflügelt ist der Bogen schnell unterschrieben.

Dann heisst es zu unserem Bedauern auch schon wieder auftauchen. Am Ende der Ausstellung erwartet uns der unvermeidliche Souvenirshop mit den ebenso unvermeidlichen Plüschschildkröten und vielem mehr.

Zugabe! Zugabe!

Aber ganz zuende ist unsere Reise doch noch nicht: Von hier aus gelangt man nämlich direkt in das Naturmuseum Bodensee im Obergeschoss, das im Eintritt zum Sea Life enthalten ist! Hier erfahren wir viel Interessantes zur Natur und Naturgeschichte der Bodenseeregion und lernen viele ihrer tierischen Bewohner anhand von sehr lebendig wirkenden ausgestopften Exemplaren kennen. Es lohnt sich wirklich, diesen Abstecher an Land zu machen.

Ausserdem: Wir haben anfangs an der Kasse Stempel auf die Hand erhalten. Mit diesen könnten wir unseren Tauchgang noch einmal von vorne beginnen, um noch mehr zu entdecken, eine weitere Fütterung zu erleben, oder… Und das den ganzen Tag lang beliebig oft.

Aber nach unserer ausführlichen Reise zieht uns nun der Hunger in eines der Restaurants am Hafen.

 

Öffnungszeiten und Eintrittspreise

Das Sea Life Center Konstanz hat jeden Tag von 10 bis 17 Uhr – im August von 10 bis 18 Uhr – geöffnet. Einzig am heiligen Abend (24.12.) bleibt das Aquarium geschlossen.

Ein Tagesticket für Erwachsene kostet an der Kasse derzeit EUR 18,75, für Kinder von 3 bis 15 Jahren rund EUR 12,86 (Kleinkinder unter 3 Jahren sind frei). Das macht den Sea Life – Besuch für Familien zu einem teuren Unterfangen. Daher zwei Spar-Tipps:

1. Bucht eure Tickets vorab online – so sind sie 30% günstiger (EUR 13,10 für Erwachsene, EUR 9,00 für Kinder, Stand September 2018).

2. Tut euch für euren Besuch mit zwei bis drei Familien zusammen, sodass ihr mindestens 10 Leute über 3 Jahren seid, und meldet euch als Gruppe an. Dann zahlt jede Person über 3 Jahren EUR 8,00.

 

Wie kommt man zum Sea Life Center?

Aus der Schweiz kommt man denkbar einfach mit dem Zug nach Konstanz: Der Hauptbahnhof Konstanz gehört – obgleich in Deutschland gelegen – quasi zum Schweizer Schienennetz. Das heisst, Billetts/Fahrkarten gibt es an den Billett-Automaten der SBB. Ausserdem bieten die SBB vorläufig bis zum 31.10.18 einen ermässigten Fahr- und Eintrittspreis als „RailAway-Kombi“ an. Und mit dem GA fahrt ihr sogar gratis bis nach Konstanz (und solltet die Eintrittskarten online direkt beim Sea Life buchen – das kommt am günstigsten).

Da ihr von der Schweiz (oder von Österreich) aus nichts desto trotz die Landesgrenze überquert: ID/Personalausweis nicht vergessen! Normalerweise bekommt ihr von der Grenzüberquerung aber gar nichts mit: Es gibt in der Regel keinerlei Grenzkontrollen – Schengenraum sei Dank.

Auch von Deutschland aus empfehle ich die Anreise mit der Bahn – das erspart euch Stadtverkehr und Parkplatzsuche. Mit dem Baden-Württemberg-Ticket für Familien könnt ihr günstig im Nahverkehr aus dem ganzen Bundesland an- und abreisen.

Vom Bahnhof sind es ca. 400m Fussweg am Hafen entlang nach Süden: Das Aquarium steht direkt am Bodensee.

Und noch einmal mein dringender Rat an alle Eltern mit Kleinkindern und Babys: Lasst den Kinderwagen wirklich draussen auf dem Kinderwagenparkplatz stehen, denn drinnen wird es eng!

 

Gesamteindruck vom Sea Life Konstanz

Das Sea Life Konstanz bietet eine aufwändig gestaltete, farbenfrohe Aquarien-Ausstellung, die uns zuweilen das Gefühl gab, durch einen Freizeitpark zu spazieren. Das reichhaltige „Drumherum“ nimmt – im Vergleich zu anderen Grossaquarien, die ich kenne, etwas den Fokus von den Tieren selbst.

Trotzdem gibt es in den Becken viele spannende und bizarre Lebewesen zu entdecken und zu bestaunen. Wie für jeden Aquarien-Besuch lohnt es sich auch hier, sich Zeit zu nehmen und aufmerksam zu beobachten, was in den Becken kreucht und….schwimmt.

Die Ausstellung ist speziell auf Primarschul- (Grundschul-) und Kindergartenkinder zugeschnitten. Dennoch kommen auch Grössere und Erwachsene auf ihre Kosten, wenn sie sich auf die bunte Tauchfahrt einlassen und gemeinsam mit den Nachwuchs-Forschern auf Entdeckung gehen. Wer detaillierte und weiterführende zoologische Informationen zu den Aquarienbewohnern schätzt, findet davon in anderen Aquarien allerdings einiges mehr.

Die Ausstellung im Sea Life Konstanz ist im Vergleich zu anderen Aquarien ziemlich eng gestaltet! An unserem gut besuchten Tag war zum Überholen auf dem linearen Weg durch die Ausstellung (um zur Pinguinfütterung zu gelangen) vielfach Geduld und Umsicht erforderlich. Trotzdem konnten wir an allen Becken beobachten ohne uns bedrängt zu fühlen. Ich zumindest habe das Aquarium nicht als überlaufen empfunden.

Grösster Wehmutstropfen sind die stolzen Eintrittspreise, die den Besuch im Sea Life für Familien schnell zur Grossinvestition werden lassen. Wenn euch die bunte Unterwasser-Expedition trotz der oben genannten Tipps zu teuer ist, könnt ihr euer Glück ja beim

 

Gewinnspiel

versuchen!

Zu gewinnen gibt es einen freien Eintritt in das Sea Life Konstanz für eure ganze Familie – inklusive einer Plüsch-Schildkröte als Andenken für eure Nachwuchs-Schildkrötenretter!

Wie ihr am Gewinnspiel teilnehmen könnt

Kommentiert dazu einfach bis zum 25. September 2018 unter diesem Beitrag und verratet uns: Was war eure bislang spannend Tier-Beobachtung im, auf oder unter Wasser (im Aquarium oder sogar draussen in der Natur)? Gebt dabei eine gültige Email-Adresse im entsprechenden Feld an, damit ich euch im Fall eines Gewinns erreichen kann!

Anschliessend werde ich den Gewinner unter allen gültigen Kommentaren auslosen.

Teilnahmebedingungen

  • Das Gewinnspiel wird von Keinsteins Kiste in Zusammenarbeit mit dem Sea Life Center Konstanz veranstaltet. Vielen Dank für die Bereitstellung und den Versand des Preises!
  • Das Gewinnspiel startet am 11. September 2018 und endet am 25. September 2018 um 24.00 Uhr.
  • Die Teilnahme am Gewinnspiel ist kostenlos.
  • Ihr müsst mindestens 18 Jahre alt sein (Liebe Kinder: Tut euch mit euren Eltern, Grosseltern oder anderen Erwachsenen zusammen!).
  • Ihr müsst eine Post-Adresse in der Schweiz, Deutschland oder Österreich haben, an welche der Gewinnpreis versandt werden kann.
  • Gewinnpreis sind Tageskarten für den Besuch des Sea Life Centers Konstanz für eine Familie plus je eine Plüsch-Schildkröte für die Kinder der Gewinner-Familie.
  • Es gibt 1 Los für einen Kommentar mit gewünschtem Inhalt (s.o.).
  • Eine Auszahlung des Gewinns in bar ist nicht möglich. Der Rechtsweg ist ausgeschlossen.
  • Der Gewinner wird ausgelost und per eMail benachrichtigt. Dabei wird er darum gebeten, der Weitergabe seiner Postadresse an das Sea Life Center Konstanz zuzustimmen, damit der Gewinn direkt vom Verlag versandt werden kann.
  • Die Gewinne gelten auf den Namen der teilnehmenden Person und sind nicht auf Drittpersonen übertragbar. Sofern die Ausschüttung eines Gewinns an einen in der Ziehung ermittelten Gewinner nicht möglich ist, weil eine Gewinnbenachrichtigung und/oder Gewinnzustellung scheitern und nicht binnen eines Monats nach der Ziehung nachgeholt werden können, verfällt der Gewinnanspruch.
  • Der Veranstalter behält sich das Recht vor, das Gewinnspiel aus sachlichen Gründen jederzeit ohne Vorankündigung zu modifizieren, abzubrechen oder zu beenden.

Ich wünsche euch viel Erfolg und viel Spass beim Lesen, Stöbern, Beobachten und Staunen!

/22 Comments/by

Abfluss und Corioliskraft – Physik für Touristen oder alles fake?

Abfluss auf Nord- und Südhalbkugel: Physik oder Fake?

Marion, eine Leserin, auf deren Blog ich schon mehr als einmal als Gastautorin gewirkt habe, schickte mir neulich einen Link zu einem Video, das gerade auf Facebook die Runde machte. Darin zu sehen sind Einwohner Kenias bzw. Tansanias, die filmenden Touristen ein Experiment vorführen. Das Spannende daran: Diese beiden Länder liegen auf dem Äquator!

Die Anrainer dieser Kreislinie, welche den Globus genau in Nord- und Südhalbkugel teilt, möchten den Touristen mit ihrem Experiment weismachen, dass Wasser, welches durch ein enges Loch abläuft, je nach Position auf der Erdkugel in eine bestimmte Richtung wirbelt: Links herum auf der Nordhalbkugel, Rechts herum auf der Südhalbkugel und genau auf dem Äquator ganz ohne Wirbel, d.h. gerade nach unten durch das Loch. Und das soll mit Hilfe eines Trichters und eines Eimers Wasser auf einem vielleicht 30 Meter langen Stück Strasse nachprüfbar sein.

„Das ist doch alles fake, oder?“, fragte mich die Leserin. Und mein Instinkt sagte gleich, dass ihrem Bauchgefühl zu trauen sei. Dennoch habe ich nachgelesen und schnell bestätigt bekommen – unter anderem in der Lehrmaterialsammlung der Uni Karlsruhe – dass Marion ganz richtig liegt: Alles fake!

Aber wie kommt es dazu, dass derlei Gerüchte um die Drehrichtung von abfliessendem Wasser sich so hartnäckig um die ganze Welt verbreiten (auch in südamerikanischen Ländern auf dem Äquator sollen entsprechende Experimente gezeigt werden)? Warum sollte das Wasser auf der Nordhalbkugel links- und auf der Südhalbkugel rechtsherum in den Abfluss wirbeln?

 

Was die Drehrichtung des Wassers bestimmen soll: Die Corioliskraft

Urheber der vorbestimmten Drehrichtung sei – so heisst es in den meisten Gerüchten – die Drehbewegung der Erde um sich selbst. Die führt nämlich wirklich dazu, dass eine geheimnisvolle Kraft – die Physiker nennen sie Corioliskraft – von der Erdkugel ausgehende Bewegungen in eine bestimmte Richtung ablenkt!

Welche Bewegungen werden abgelenkt?

Die Corioliskraft wirkt auf solche Bewegungen, die von einem Pol zum anderen, also entlang der Längengrade (jener Linien, die auf der Weltkarte oder dem Globus Nord- und Südpol miteinander verbinden) oder von der Drehachse der Erde fort bzw. zu ihr hin (aus Sicht eines Menschen auf der Erdoberfläche „nach oben“ oder „nach unten“ verlaufen.

Wie kommt es zu der Ablenkung?

Die Erdumdrehung als Ursache

Die Erde ist (mehr oder weniger) eine Kugel, die sich stetig um ihre Mittelachse dreht – also um die gerade Linie, die Nord- und Südpol durch die Kugel hindurch miteinander verbindet. Da diese Erdkugel im Grossen und Ganzen ein fester Körper ist, müssen sich alles Material, aus dem sie besteht und alles, was sonst noch darauf haftet (Meere, Pflanzen, Tiere, Menschen und sogar die Lufthülle, die den Planeten umgibt!) stets im gleicher Lage zueinander mitdrehen, damit alles seinen Platz behält. Schliesslich ist es noch nie vorgekommen, dass jemand seine Fortbewegung durch die Erddrehung verschlafen hätte und ein paar Tausend Kilometer weiter westlich wieder aufgewacht wäre.

Alle Orte auf der Erde drehen sich gemeinsam

Dieser feste Zusammenhalt aller Teile der Erdkugel führt auch dazu, dass die Entfernung zwischen Tunis, der Hauptstadt Tunesiens in Nordafrika, und der Norwegischen Hauptstadt Oslo zu jeder Tages- und Nachtzeit gleich ist. Wenn ihr nun Tunis und Oslo auf einem Globus-Modell ausfindig macht (beide Städte liegen nahezu auf demselben Längengrad!) und kleines Bisschen von Physik versteht, mag euch eine Ungereimtheit ins Auge fallen:

Nicht alle Punkte auf der Erdoberfläche drehen sich gleich schnell

Tunis liegt deutlich weiter aussen auf der Wölbung des Globus‘ als Oslo, d.h. der Abstand von Tunis zur Mittelachse ist deutlich grösser als der Abstand von Oslo zur Mittelachse. Das bedeutet, dass der Kreis, welchen Tunis innerhalb eines Tages entlang bewegt wird, erheblich länger ist – d.h. einen grösseren Umfang hat – als der Kreis, welchen Oslo entlang bewegt wird!

Vom Abstand zum Kreisumfang

Die Länge einer Kreislinie, d.h. den Umfang U eines Kreises kann man berechnen, indem man seinen Radius r – den Abstand zwischen Kreislinie und Kreismittelpunkt – mit 2 und der Zahl Pi multipliziert.

Damit entspricht der (kürzeste) Abstand von Tunis bzw. Oslo zur Drehachse der Erde dem Radius, aus dem sich die Länge des Umlaufs der jeweiligen Stadt während eines Tages ergibt.

Damit die Entfernung zwischen beiden Städten stets gleich bleibt, müssen sowohl Tunis als auch Oslo sich an einem Tag (d.h. in 24 Stunden) genau einmal um die Erdachse wandern. Wegen des grösseren Abstands zur Drehachse muss Tunis dazu einen längeren Weg zurücklegen als Oslo. Das bedeutet: Tunis muss sich schneller bewegen als Oslo, um seine längere Umlaufstrecke am gleichen Tag zu schaffen!

Geschwindigkeit und Drehgeschwindigkeit

Die Geschwindigkeit v einer gleichförmigen, d.h. stetig in die gleiche Richtung verlaufenden Bewegung kann man ausrechnen, indem man einen zurückgelegten Streckenabschnitt durch die dafür benötigte Zeitspanne teilt:

Eine vergleichbare Beziehung gilt auch für eine gleichförmige Kreisbewegung, in welcher der zurückgelegte Winkel Phi (φ) den Streckenabschnitt ersetzt. Die so berechnete Grösse nennen die Physiker Dreh- oder Winkelgeschwindigkeit und schreiben dafür statt v ein kleines Omega (ω):

Wenn die benötigte Zeit für zwei Bewegungen gleich ist, aber ein Streckenabschnitt bzw. Winkel grösser als der andere, ergibt sich mit dem somit grösseren Zähler im Bruch auf der rechten Seite der Gleichung aus dem grösseren Streckenabschnitt bzw. Winkel eine grössere Geschwindigkeit.

Gut sichtbar wird das, wenn ihr euch die Erdkugel einmal von „oben“ anseht:

Ablenkung eines Balls auf dem Weg von Oslo nach Tunis

Die Erde von einem Punkt über dem Nordpol aus gesehen: Die Nordhalbkugel erscheint als flache Scheibe mit dem Nordpol als Mittelpunkt. Ein Fussball fliegt von Oslo in der Nähe des Mittelpunkts nach Tunis, welches weiter vom Mittelpunkt entfernt liegt. Aus der Summe der Geschwindigkeiten von Oslo (kurzer blauer Pfeil) und der Südwärtsbewegung des Balles (durchgezogener roter bzw. langer blauer Pfeil) ergibt sich Punkt (2) als Zielpunkt für den Ball. Tunis, das sich schneller als Oslo bewegen muss, um seinen längeren Kreisabschnitt in gleicher Zeit zu schaffen, befindet sich dann aber schon an Punkt (3)! Der Weg des Balls kann auch durch die gekrümmte gepunktete Linie beschrieben werden: Eine Kraft – die Corioliskraft, die nach „rechts“ wirkt, lenkt den Ball von der geraden Flugbahn ab.

Die Grafik zeigt die Erde aus der Sicht eines Astronauten, der über dem Nordpol (in der Grafik der Mittelpunkt der Kreise) schwebt. Die gestrichelte Kreisline markiert den Weg, auf dem sich Oslo mit der Erde dreht. Die mittlere, durchgezogene Kreislinie zeigt den Weg, den Tunis nimmt (da Tunis auf der Kugelwölbung weiter aussen liegt, ist dieser Kreis grösser). Der ganz äussere Kreis ist der Äquator – die Südhalbkugel ist aus dieser Richtung nicht zu sehen.

Ein Fussballspiel von Oslo nach Tunis

Stellt euch nun vor, ein besonders kräftiger Spieler würde einen Fussball vom Anstosspunkt im Osloer Stadion über die Stadionmauer in Richtung Tunis (also genau nach Süden) treten. Wenn der Fussballspieler nun als Kind in den Zaubertrank gefallen ist und der Ball seine Reise über Europa hinweg antritt…wo würde er dann – die Lufthülle der Erde mal ausser Acht gelassen – landen? Im Tor im Stadion von Tunis?

Die Krux mit der Impulserhaltung

Eines der grundlegenden Gesetze der Physik – das Gesetz der Impulserhaltung – schreibt vor, dass jede Bewegung eines jeden Gegenstands in jede Richtung erhalten bleibt, so lange keine Kraft in die der Bewegung entgegengesetzte Richtung wirkt und ihn ausbremst.

Da der Fussball vor dem Anstoss auf der Erde gelegen hat, hat er sich zunächst mit der Geschwindikgeit von Oslo um die Erdachse gedreht. Diese Drehrichtung und -geschwindigkeit bleibt dem Ball auch, nachdem der Fussballer ihn in Richtung Süden getreten hat. Die Bewegung in Richtung Süden wird einfach zur Bewegung in Richtung der Oslo-Kreisbahn hinzugezählt.

Wie man Bewegungen addiert

Die geraden Pfeile in der Grafik zeigen die Richtungen der Teilbewegungen an – die Länge der Pfeile steht für die Geschwindigkeit bzw. den Impuls in der jeweiligen Richtung. Verschiebt man nun das hintere Ende eines Pfeils an die Spitze des ersten, zeigt der neue Pfeil vom hinteren Ende des einen zur Spitze des anderen Pfeils die Richtung der Gesamtbewegung (und dessen Länge die Gesamtgeschwindigkeit). Dieses Verfahren nennen die Mathematiker Vektoraddition (denn die Pfeile heissen bei ihnen Vektoren).

Die Grafik zeigt: Obwohl nach Süden getreten bewegt sich der Fussball diagonal über Europa nach Südosten – wobei die Geschwindikeit in Ost-Richtung der von Oslo entspricht. Damit landet der Ball am Punkt 2 irgendwo an der tunesischen oder algerischen Mittelmeerküste und nicht in Tunis (das befindet sich inzwischen weiter östlich an Punkt 3). Denn weil Tunis sich schneller bewegt als Oslo, ist es während der Flugzeit des Fussballs weiter nach Osten gewandert als der von der Impulserhaltung als „südlich von Oslo“ vorgegebene Punkt 2! Der Schuss geht also gründlich daneben.

Durch Drehbewegung auf die krumme Bahn

Wenn der Astronaut, der über dem Nordpol unbewegt schwebt, dieses unglaubliche Fussballspiel beobachtet und filmt, um anschliessend die Position des Balles in regelmässigen Zeitabschnitten einzublenden, erhält er eine Linie, die dem nach links gekrümmten gestrichelten Pfeil in der Grafik entspricht. Solch eine gekrümmte Flugbahn lässt sich mathematisch beschreiben, indem man annimmt, dass eine Kraft den Fussball in Ablenkungsrichtung beschleunigt – die sogenannte Corioliskraft.

Kraft und Beschleunigung: Zwei physikalische Grössen mit Richtung

Das Grundgesetz der Mechanik beschreibt die einfache Beziehung zwischen Kraft (F) und Beschleunigung (a):

Je grösser die Kraft ist, die auf einen Gegenstand mit der Masse m wirkt, desto grösser ist dessen Beschleunigung – d.h. desto schneller wird der Gegenstand schneller. Die physikalische Grösse für die Beschleunigung ist – wie auch jene für die Geschwindigkeit – stets mit einer Richtung versehen, die gemäss der Gleichung auch für die Kraft gilt.

Da die Corioliskraft mathematisch nur „in Erscheinung tritt“, wenn man das Fussballspiel wie der Astronaut von aussen beobachtet (die Zuschauer im Stadion in Oslo, die vor dem Abstoss mit Stadt und Ball um die Erdachse kreisen, kommen mit Hilfe der Vektoraddition weiter oben auf das Ziel des Balles), wird sie von den Physikern eine Scheinkraft genannt.

Die Corioliskraft ist aber durchaus real

Trotzdem könnt ihr selbst die Corioliskraft spüren, wenn ihr zum Beispiel versucht, auf einer sich drehenden Karussell-Scheibe auf dem Spielplatz geradewegs zu ihrem Mittelpunkt zu laufen. Das ist nämlich gar nicht so einfach – ihr müsst schon ordentlich gegenhalten, damit euch die Corioliskraft nicht von eurem direkten Weg ablenkt!

Ähnlich verhält es sich auch mit unserem unwahrscheinlichen Fussballspiel: Wenn die tunesische Küstenwache den Fussball aus dem Mittelmeer fischen und ins Stadion von Tunis bringt, sodass ein wiederum sehr starker Spieler den Ball in Richtung Oslo abstossen kann, würde auch er das Tor der Norweger nicht treffen. Denn da der Ball nun die höhere Drehgeschwindigkeit von Tunis mitnimmt, wird das langsamere Oslo den durch die Addition der Teilbewegungen ermittelten Zielpunkt beim Eintreffen des Balls noch nicht erreicht haben: Stattdessen fällt der Ball weiter östlich vielleicht auf die Grenze zwischen Norwegen und Schweden.

Die Regeln für die Ablenkung durch die Corioliskraft

Ganz gleich, in welche Richtung der Ball auf der Nordhalbkugel gespielt wird: In Flugrichtung gesehen lenkt die Corioliskraft den Ball stets „nach rechts“ (d.h. in Nord-Süd-Richtung nach Westen und in Süd-Nord-Richtung nach Osten).

Würde man ein ebenso unwahrscheinliches Fussballspiel auf der Südhalbkugel austragen, müsstet ihr die Zeichnung oben in einem Spiegel betrachten: An die Stelle des Nordpols tritt der Südpol (der ist auch auf jeder europäischen Landkarte unten, sodass ihr euren Atlas nun richtig herum halten könnt) und Osten ist nun rechts, sodass die Erde sich nun rechts herum dreht. Demnach „wirkt“ auch die Corioliskraft nun in spiegelverkehrter Richtung:

Ganz gleich, in welche Richtung der Ball auf der Südhalbkugel gespielt wird: In Flugrichtung gesehen lenkt die Corioliskraft den Ball stets „nach links“ (d.h. in Nord-Süd-Richtung nach Osten und in Süd-Nord-Richtung nach Westen).
Warum das unwahrscheinliche Fussballspiel?

Vielleicht habt ihr euch schon gefragt, weshalb ich so eine hanebüchene Begebenheit wie ein Fussballspiel von Oslo nach Tunis ersinne, um die Ablenkung durch die Corioliskraft zu beschreiben. Würden realistischere Umstände nicht den gleichen Zweck erfüllen?

Mit dieser klugen Frage kommen wir zu den Wasserwirbeln in Kenia und Tansania zurück. Der gekrümmte Pfeil in der Grafik deutet es schon an: Da die Ablenkung durch die Corioliskraft auf unterschiedlichen Geschwindigkeiten von Start- und Zielort einer Bewegung beruht, fällt eben diese Ablenkung um so grösser aus, je grösser der betreffende Geschwindigkeitsunterschied ist. Und der Geschwindigkeitsunterschied ist um so grösser, je weiter die Abstände von Start und Ziel von der Drehachse sich unterscheiden – d.h. je weiter Start und Ziel in Nord-Süd-Richtung voneinander entfernt liegen!

 

Warum die Corioliskraft für das Abfluss-Experiment keine Bedeutung hat

Beim Abfliessen aus einem vielleicht 40cm durchmessenden Trichter kommen die strömenden Wasserteilchen auf eine Bewegung von höchstens 20 Zentimeter in Nord-Süd-Richtung und wieder zurück. Dementsprechend winzig ist der Einfluss der Corioliskraft auf die Bewegungsrichtung der Teilchen – und dementsprechend einfach lässt sich die Bewegung durch andere Kräfte sehr gezielt beeinflussen.

Solche Kräfte lassen sich zum Beispiel durch eine angepasste Trichterform ausüben, welche die daran vorbei strömenden Wasserteilchen ganz unscheinbar in die gewünschte Richtung lenkt. Die Bemalung mit den auffälligen Spiralmustern lenkt recht erfolgreich von diesen kleinen Unterschieden ab.

Wenn ihr genau hinschaut, könnt ihr im Video erkennen, dass der Trichter, der „auf dem Äquator“ zum Einsatz kommt (welcher übrigens den Wirbel mittig halbiert, sodass die entgegengesetzte Wirkung der Coriolis-Ablenkung in der Nord- und Südhälfte sich aufheben soll), eine andere Form zu haben scheint als die Trichter für den Norden und den Süden.

 

Wo ihr die Auswirkung der Corioliskraft wirklich beobachten könnt

Wenn bei der Wettervorhersage im Fernsehen eine bewegte Wetterkarte zum Einsatz kommt, sind darauf meist riesige Wolkenwirbel zu sehen, die sich in die eine oder andere Richtung drehen. Es handelt sich dabei um Gebiete mit besonders hohem oder besonders tiefem Luftdruck. Ein hoher Luftdruck führt dazu, dass Luft in alle Richtungen von dem Gebiet wegströmt, während tiefer Luftdruck dazu führt, dass aus allen Richtungen zum betreffenden Gebiet hinströmt.

Diese Luftströmungen sind Hunderte bis Tausende Kilometer lang – und da die Lufthülle des Planeten sich im Grossen und Ganzen mit der Erde mitdreht, wirkt auf die strömenden Teilchen eine Corioliskraft. Die führt dazu, dass die Luftströme nicht geradlinig auf ein „Tief“ zu oder von einem „Hoch“ weg strömen, sondern in krummen, einen abflussähnlichen Wirbel bildenden Bahnen.

Der Coriolis-Ablenkung wegen drehen sich die Wirbel um Hochdruckgebiete auf der Nordhalbkugel stets „nach rechts“, also im Uhrzeigersinn, während die Wirbel um Tiefdruckgebiete – hier strömt die Luft in umgekehrter Weise – sich stets „nach links“, also gegen den Uhrzeigersinn drehen. Auf der Südhalbkugel, wo die Corioliskraft in seitenverkehrter Weise wirkt, ist das genau umgekehrt.

Um dagegen die Wirkung der Corioliskraft auf Wasserwirbel sichtbar zu machen, müssen diese mindestens ein paar Meter durchmessen und in aufwändig vor äusseren Einflüssen geschützter Umgebung im Labor kreisen können – auf der Strasse in Kenia funktioniert das jedenfalls nicht!

Seid ihr dem Mythos um die Drehrichtung von abfliessendem Wasser auch schon begegnet?

Und wenn ihr anlässlich der kommenden Weltmeisterschaft nur noch Fussball im Kopf habt, habe ich auch eine passende Anekdote aus der Chemie: Die Natur hat nämlich ein originalgetreues Fussball-Molekül erfunden!

/4 Comments/by

Experimente : Harry Potter-Zauber dank Oberflächenspannung

Experimente Zauber mit Oberflächenspannung

In der Schweizer Fasnacht sind Hexen zentrale Figuren, aber bestimmt sind auch Zauberer, Feen und andere magische Wesen bei der Kostümwahl beliebt. Mache dein magisches Kostüm wirklich einzigartig: Ich verrate dir, wie du wirklich zaubern und deine Freunde und (Mit-)Gäste verblüffen kannst! Die Physik bzw. Chemie machts möglich!

 

1. Die schwimmende Büroklammer

Du brauchst dazu

  • ein sauberes Glas mit Leitungswasser
  • ein wenig Flüssigseife
  • eine Büroklammer
  • eine Pinzette
  • deinen Zauberstab

 Material für Büroklammer vs. Oberflächenspannung

Wie du den Zauber durchführst

  • präpariere den Zauberstab, bevor die Zuschauer dabei sind: Gib ein wenig Flüssigseife auf die Spitze, sodass das nicht auffällt
  • In Gegenwart der Zuschauer: Lege die Büroklammer mit Hilfe der Pinzette vorsichtig auf die Oberfläche des Wassers im Glas. Die Klammer wird schwimmen.
  • Bereite dich mit dem nötigen Brimborium aufs Zaubern vor
  • Führe den Zauberstab dabei nahe an die WasseroberflächeAlles bereit: Jetzt dein Zauberspruch!
  • Tippe, während du deinen Zauberspruch sagst, mit der seifigen Spitze des Stabes 1 – 2 cm von der Büroklammer entfernt auf die Wasseroberfläche. Klammer wird sofort auf den Grund des Glases sinken.Keine Oberflächenspannung mehr: Die Klammer ist versunken!

 

Was passiert da?

Wenn du schon das letzte Experiment rund um die Dichte und die Anomalie des Wassers gelesen hast, wirst du wissen: Nur Dinge, deren Dichte kleiner ist als die von flüssigem Wasser, können darauf schwimmen. So sollte es jedenfalls sein. Trotzdem schwimmt die Büroklammer aus Metall (zum Beispiel Eisen), dessen Dichte um ein Vielfaches höher als die flüssigen Wassers ist!

Die Oberflächenspannung machts möglich

Das rührt daher, dass Wasserteilchen ausserordentlich fest zusammenhalten. Zwischen den Wasserteilchen bzw. -molekülen wirken auch im flüssigen Zustand stark anziehende Kräfte, die sogenannten Wasserstoffbrücken, welche auch einen weiteren Zaubertrick – Harry Potter und der krumme Wasserstrahl – möglich machen. Dank dieser Wasserstoffbrücken halten die Wasserteilchen so dicht zusammen, dass sie an der Luft (mit welcher Wasserteilchen so gar nicht wechselwirken mögen) eine relativ schwer zu durchdringende Oberfläche bilden.

Diese Oberfläche ist so stabil, dass sie sogar der Erdanziehung standhalten kann: Wassertropfen zerlaufen auf einer Unterlage nicht, um der Schwerkraft folgend möglichst flach zu werden. Stattdessen erscheinen sie gewölbt (dazu findet ihr ein Experiment bei Forschen für Kinder)! Wie die Haut eines aufgeblasenen Luftballons steht die Wasseroberfläche dabei unter Spannung. Deshalb wird diese fesselnde Eigenschaft des Wassers (und anderer Stoffe) „Oberflächenspannung“ genannt.

Dank der grossen Oberflächenspannung des Wassers können auch kleine Eisenteile schwimmen, obwohl sie eigentlich zu dicht dafür sind – wenn ihr Gewicht, wie bei der Büroklammer, auf genügend Auflagefläche verteilt wird. So ist nämlich an keiner Stelle die Last gross genug, um die film-artige Wasseroberfläche zu durchbrechen.

Die Zauberkraft der Tenside

Seife – nicht nur flüssige – besteht aus Tensiden. Das sind ganz besondere Teilchen: Sie haben nämlich zwei unterschiedliche Enden, die mit unterschiedlichen wechselwirken! Das macht die Tenside zu kleinen Diplomaten. Während nämlich das eine Ende Wasserteilchen anzieht und von ihnen angezogen wird, pflegt das andere Ende anziehende Wechselwirkungen mit solchen Teilchen, die sich nicht gern mit Wasser mischen.

Das verleiht den Tensiden nicht nur ihre Super-Waschraft, die darauf beruht, dass sie zwischen Wasser und Fett „vermitteln“ und dem Fett ermöglichen, sich mit Wasser zu mischen. Tenside vermitteln nämlich ebenso zwischen Wasser und Luft – die sich in Bezug auf Wechselwirkungen wie Fett verhält, nämlich wasserabweisend.

Was dein Zauber bewirkt

Wenn du mit der Seife am Zauberstab auf die Wasseroberfläche tippst oder kurz hinein tauchst, lösen sich die Tenside vom Stab und ordnen sich an der Wasseroberfläche an: (wasserliebendes) Köpfchen in das Wasser, (fett- bzw. luftliebendes) Schwänzchen in die Höh!

Streichholzmodell: Tenside an der Wasseroberfläche

Dadurch wird der Zusammenhalt zwischen den einzelnen Wasermolekülen minimiert, wenn nicht gar aufgehoben, sodass die Oberflächenspannung zusammenbricht. Ohne den festen Oberflächenfilm ist nichts mehr da, was die Büroklammer tragen könnte, sodass sie wie ein Stein auf den Grund sinkt, wie ihre Dichte es vorschreibt.

2. Der furchtsame Pfeffer

Du brauchst dazu

  • ein sauberes Glas mit Leitungswasser
  • gemahlenen Pfeffer oder ein anderes wasserunlösliches Pulver
  • Flüssigseife
  • deinen Zauberstab

Material für den Zauber mit Pfeffer

Wie du den Zauber durchführst

  • Bringe wie im 1. Versuch vorab ein wenig Flüssigseife auf die Spitze deines Zauberstabs.
  • Wenn die Zuschauer da sind, bestreue die Wasseroberfläche auf dem Glas dicht mit gemahlenem Pfeffer. Das Pulver wird auf der Wasseroberfläche schwimmen.Pfeffer schwimmt auf der Wasseroberfläche
  • Bereite dich mit dem nötigen Brimborium aufs Zaubern vor. Bringe dabei den Zauberstab in die Nähe der Wasseroberfläche.
  • Wenn du deinen Zauberspruch sagst, tippe die Stabspitze kurz – für höchstens ein bis zwei Sekunden – auf die Wasseroberfläche. Die Pulverkörner auf der Wasserfläche werden sofort vor der Stabspitze Reissaus nehmen und in Richtung der Glasränder drängen!Der Pfeffer flieht vor dem Zauberstab!

Was passiert da?

Es sind einmal mehr die Tenside, welche die Pfefferkörnchen zur Flucht bewegen. Wie eine Schar, die auseinanderstrebt, breiten sich die Seifenteilchen vom Zauberstab fort auf der Wasseroberfläche aus. Dabei schieben sie die schwimmenden Pulverkörner kurzerhand zur Seite.

Da wir die winzigen Seifenteilchen nicht sehen können, erscheint dies so, als würden die sichtbaren Pulverkörner vor dem Stab zurückweichen!

Damit dir und allen anderen Lesern ein fröhliches Ohhh Häx!, Helau!, Alaaf!, Narri! Narro! und was man durch die Länder sonst noch alles ruft!

Hast du das Experiment nachgemacht: 

[poll id=“25″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/0 Comments/by

Experiment : Wasser und seine Dichteanomalie – Eis wächst!

gefrorenes Wasser : Das Glas wird voller

Warum ist es eigentlich keine gute Idee, eine geschlossene Glasflasche mit Wasser ins Tiefkühlfach zu legen? Dieses Experiment zeigt euch eine ungewöhnliche, verblüffende Eigenschaft des Wassers – seine Dichteanomalie!

Der Januar war hier in den niedrigen Regionen der Schweiz viel zu warm, aber der Februar grüsst heute Morgen mit einer feinen Puderzucker-Schneeschicht. So könnt ihr in diesem Winter vielleicht doch noch Beobachtungen machen, die spannende Fragen aufwerfen: Warum friert bei einem Teich zuerst die Oberfläche zu, während das Wasser darunter flüssig bleibt? Und warum sieht ein Wasserkübel voller aus, wenn das Wasser darin zu Eis erstarrt?

Dass der Kübel tatsächlich voller ist, könnt ihr mit diesem einfachen Experiment nachweisen!

Ihr braucht dazu

  • Ein – möglichst schmales – Trinkglas, das in euer Tiefkühlfach passt
  • Ein Tiefkühlfach (wenn es draussen friert, genügt auch Platz auf Balkon oder Terrasse)
  • Kaltes Leitungswassser
  • Einen wasserfesten Filzstift
  • Ein Lineal
  • Optional: Gefäss mit Skala und eine Küchen- oder Laborwaage
Material für das Experiment
Das ist alles was ihr braucht, um Wasser wachsen zu lassen!

Wie ihr das Experiment durchführt

  • Füllt das Glas etwa zwei Drittel hoch mit Leitungswasser und stellt es auf eine waagerechte Fläche.
  • Markiert die Höhe des Wasserspiegels mit einem Filzstift-Strich. Mit dem Lineal könnt ihr die Füllhöhe zudem auch in Zentimetern messen.
  • Stellt das Glas mit dem Wasser in euer Tiefkühlfach oder bei Frost nach draussen und wartet einige Stunden.
  • Wenn das Wasser vollständig gefroren ist, nehmt das Glas wieder aus dem Tiefkühlfach bzw. nach drinnen und wartet wenige Minuten, bis die Luftfeuchtigkeit nicht mehr sofort einen weissen Schleier auf der Glasoberfläche bildet. Wischt eventuelle Reste dieses Schleiers ab (gebt dabei acht, dass der Filzstift-Strich erhalten bleibt!).
  • Vergleicht die Höhe der Eissäule im Glas mit eurer Markierung. Mit dem Lineal könnt ihr den Höhenunterschied in Millimetern messen!

Wenn ihr eine Waage und ein Gefäss mit unterteilter Skala, zum Beispiel einen Messzylinder, habt, könnt ihr auch die Veränderung der Dichte des Wassers messen:

  • Wiegt das Glasgefäss vor und nach dem Einfüllen des Wassers. Der Gewichtsunterschied entspricht der Masse des eingefüllten Wassers. Lest dann das Volumen des eingefüllten Wassers (in Millilitern oder Kubikzentimetern cm3) von der Skala des Gefässes ab. Notiert beide Werte.
  • Um die Dichte des Wassers zu erhalten, teilt die Masse des Wassers durch sein Volumen (die Zahlen werden sich sehr ähneln, sodass das Ergebnis in der Nähe von 1 g/cm3 liegen wird).
  • Nachdem das Wasser gefroren ist, lest das Volumen noch einmal ab (wenn die Oberfläche der Eissäule sich gewölbt hat, versucht den Wert zu schätzen!) und rechnet die Dichte des Eises wie in 2. aus (ein zweites Mal wiegen müsst ihr dazu nicht – die Masse des Wassers ändert sich nicht!).

 

Was ihr beobachten könnt

Nach dem Gefrieren reicht die Oberfläche der Eissäule deutlich über den ursprünglichen Wasserspiegel hinaus: Eis nimmt mehr Platz ein als das flüssige Wasser, aus dem es entsteht – das Wasser ist beim Einfrieren gewachsen! In meinem Glas ist die Eissäule ganze 8 Millimeter (wenn ich zudem die Wölbung berücksichtige, mindestens 1 Zentimeter) höher als das Wasser, das ich eingefüllt hatte!

Dichteanomalie sichtbar gemacht: Das Wasser ist gewachsen!

Wenn ihr die Dichte von Wasser und Eis bestimmt, werdet ihr feststellen, dass der Wert für das Eis etwas kleiner ist als der für das Wasser (die Masse bleibt dabei unverändert: Vor und nach dem Gefrieren ist (annähernd) gleich viel Wasser im Glas).

Wie kann Wasser wachsen, wenn es friert?

Nur ganz wenige Stoffe können das. Normalerweise werden Stoffe grösser, je wärmer sie werden. Das rührt daher, dass die Teilchen in warmen Stoffen sich heftiger bewegen als die gleichen Teilchen in kalten Stoffen. Und was ständig herumzappelt oder gar -wuselt, braucht einfach mehr Platz. Das heisst auch, dass diese Stoffe kleiner werden, wenn man sie abkühlt – also auch, wenn sie gefrieren.

Wasser und einige wenige Stoffe, wie die Elemente Bismut, Gallium, Germanium, Plutonium, Silicium und Tellur , fallen da allerdings aus dem Rahmen: Sie werden mitunter grösser, wenn sie abkühlen.

Wasser verhält sich nicht „ganz normal“

Flüssiges Wasser verhält sich genaugenommen ganz normal, so lange seine Temperatur über rund 4°C liegt. Dann gilt auch hier: Je wärmer das Wasser ist, desto wuseliger sind die Teilchen, aus denen es besteht, und desto mehr Platz nimmt es ein. Oder umgekehrt: Je kälter das Wasser ist, desto weniger wuseln die Teilchen und desto weniger Platz nehmen sie ein.

Bei rund 4°C passiert dann etwas neues: Wenn das Wasser noch kälter wird, bereiten die Wasserteilchen sich darauf vor, Eiskristalle zu bilden: Sie rotten sich zusammen und bewegen sich nurmehr in der Nähe der Plätze, die sie in einem Eiskristall-Gitter einnehmen würden. So wie Kinder, die „die Reise nach Jerusalem“ spielen und – wenn sie erwarten, dass die Musik abbricht – darauf aus sind, in der Nähe der freien Stühle zu sein.

Und das Eiskristall-Gitter hat es in sich: Das Muster , in dem die Wasserteilchen darin angeordnet werden, ist nämlich ziemlich grobmaschig. Die anziehenden Wechselwirkungen, „Wasserstoffbrücken“ genannt, welche die Wasserteilchen im Gitter zusammenhalten, halten sie nämlich gleichzeitig ziemlich auf Abstand voneinander.

Ein Modell des Eiskristall-Gitters : Jeder schwarze Knoten ist ein Wasserteilchen. Die Wasserstoffbrücken – dargestellt als grüne Streben – halten die Teilchen auf Abstand!

So kommt es, dass die Wasserteilchen schon beim Zusammenrotten vor dem Gefrieren auf Abstand gehen – so wie es die spielenden Kinder wohl täten, wenn man die freien Stühle voneinander entfernt aufstellen würde. Deshalb braucht flüssiges Wasser zunehmend mehr Platz, wenn es kälter als 4°C wird.

Unmittelbar vor dem Gefrieren sind die Wasserteilchen am weitesten – also entsprechend der Maschen im Eiskristallgitter – verteilt und nehmen schliesslich ihre festen Plätze im Gitter ein: Wenn Wasser einmal erstarrt ist, wächst das Eis nicht mehr weiter!

Weil das „Wachsen“ eines abkühlenden Stoffes im Vergleich zu den meisten anderen Stoffen nicht ganz normal ist, nennen Chemiker und Physiker diese ungewöhnliche Eigenschaft eine Dichteanomalie.

Dichte – und warum Teiche stets von oben zufrieren

Der eingefrorene Wasserkübel sieht also nicht nur voller aus – er ist tatsächlich voller! Man kann das Ganze jedoch auch aus einem anderen Blickwinkel betrachten:

Würde die Wasserteilchen in einem Milliliter kaltem Wasser zählen und ihn dann einfrieren, dann wäre der entstehende Eisklumpen grösser. Um einen ordentlichen Vergleich anzustellen, könnte man aus diesem Eisklumpen einen Eiswürfel herausschneiden, der einen Milliliter fasst (das Volumen des Eiswürfels beträgt einen Milliliter). Würde man die Teilchen in diesem Eiswürfel zählen, wäre das Ergebnis eine kleinere Zahl als für einen Milliliter flüssiges Wasser – denn die Wasserteilchen, die nach dem Wachsen keinen Platz mehr im Würfel fanden, hat man schliesslich vorher weggeschnitten.

Da man mit dem Zählen von Stoffteilchen aber eine schiere Ewigkeit beschäftigt wäre, ist es wesentlich praktischer, die Teilchen alle zusammen zu wiegen. Denn jedes Teilchen hat seine Masse, die es zur Gesamtmasse eines Milliliters beisteuert. Da in einem Milliliter Eis weniger Teilchen sind, als in einem Milliliter flüssigen Wassers, wiegt ein Milliliter Eis entsprechend weniger.

Um diese veränderliche Eigenschaft von Stoffen zu beschreiben, verwenden Physiker die „Dichte“: Sie geben die Masse für ein bestimmtes Volumen des jeweiligen Stoffes an: rho = m/V . Damit lassen sich verschiedene Gesetzmässigkeit einfach ausdrücken: Aus „die meisten (flüssigen) Stoffe werden um so kleiner, je kälter sie werden“ wird so „die Dichte der meisten (flüssigen) Stoffe nimmt zu (d.h. mehr Teilchen drängen sich in einem festgelegten Volumen zusammen – das Volumen wird schwerer), wenn sie kälter werden“.

Warum Eis schwimmt

Die wenigen Stoffe, für die das nicht uneingeschränkt gilt, weisen damit eine Dichteanomalie auf. Dieser Anomalie wegen hat Eis eine geringere Dichte als Wasser.

Und damit kommen wir zu einer weiteren Gesetzmässigkeit über die Dichte von Stoffen: Füllt man zwei Stoffe (davon ist mindestens einer flüssig und keiner ein Gas) mit unterschiedlicher Dichte, die sich nicht vollständig mischen, in ein Gefäss, dann schwimmt der Stoff mit der geringeren Dichte oben.*

*Tatsächlich gilt dies nur unter Vernachlässigung einiger äusserer Umstände, zu denen ihr bald hier mehr erfahren könnt.

Das gilt natürlich auch für Eis und Wasser – deshalb schwimmen die Eiswürfel im gekühlten Drink stets obenauf!

Warum Teiche von oben einfrieren

Darüber hinaus gilt das Gesetz auch innerhalb ein und desselben flüssigen Stoffs, wenn dieser in verschiedenen Bereichen eine unterschiedliche Dichte hat (weil diese Bereiche unterschiedlich warm sind). Wenn ein anfangs warmer Teich abkühlt, ordnet sich das kalte Wasser (das die höhere Dichte hat) unterhalb des wärmeren Wassers (mit niedrigerer Dichte) an. Da Wasser bei rund 4°C die höchste Dichte hat, landet das 4°C kalte Wasser somit ganz unten – darüber sind die Schichten wärmer.

Wenn es nun im Winter richtig kalt wird, kühlen die oberen Wasserschichten unter 4°C ab. Der Dichteanomalie wegen nimmt ihre Dichte dabei jedoch ab – und die kalten Schichten bleiben oben. Mehr noch: Die kälteste Sicht – mit der geringsten Dichte – ordnet sich ganz oben an, und erstarrt dort schliesslich als erstes zu Eis.

Wasser im Teich nach Dichte sortiert
Dichteverteilung im Teich: Links wenn es warm ist: unten – bei 4° ist das Wasser am dichtesten. Rechts wenn es kalt ist: Das dichteste Wasser ist unten – kälteres Wasser ist weniger dicht! By Klaus-Dieter Keller, details from KnowItSome, Tango! Desktop Project, Julo, Spax89 [CC BY-SA 3.0], via Wikimedia Commons

So freuen wir uns, wenn wir auf der Teichoberfläche Schlittschuh laufen können, während die Fische darunter sicher sein können, flüssiges Wasser zum Schwimmen und Atmen zu finden, wenn sie nur nach ganz unten tauchen (so lange der Teich nicht komplett durchfriert).

Dank der Dichteanomalie des Wassers können nicht nur Fische den Winter überleben – womöglich hat auch das Leben auf der Erde dank dieser ungewöhnlichen Eigenschaft mehrere Eiszeiten überdauern können – sodass wir die Anomalie heute in einem Glas im Tiefkühlfach beobachten können. Spannend, nicht?


Und nun zum Abschluss eine Quizfrage: Welche „äusseren Umstände“ führen dazu, dass das Gesetz „der Stoff mit der geringeren Dichte schwimmt oben“ in Wirklichkeit mehr eine Faustregel ist, die oftmals nicht streng zu gelten scheint?

Die Auflösung samt einem spannenden Experiment gibt es nächste Woche hier in Keinsteins Kiste!

Hast du das Experiment nachgemacht: 

[poll id=“26″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/3 Comments/by

Experiment: Harry Potter und der krumme Wasserstrahl

Wasser ist spooky: Ein Zaubertrick für Gross und Klein

Bald ist Halloween: Für viele kleine und grosse Hexen und Zauberer rückt damit ein grosser Tag immer näher. Aber was wäre, wenn ihr im schaurig-schönen Kostüm auch tatsächlich zaubern könntet? Ich habe einen einfachen, aber verblüffenden Zauber für euch, mit dem ihr an eurer Halloween-Party sicher für Aufregung sorgen könnt! Und um Ärger mit dem EZD (dem Eidgenössischen Zauberei-Departement…) zu vermeiden, gibt’s auch eine wasserdichte naturwissenschaftliche Erklärung dazu.

Von Harry Potter zum verhexten Wasser

Bestimmt kennst du Harry-Potter – und vielleicht auch seine wilde Begegnung mit einem Drachen in „Harry Potter und der Feuerkelch“. Um eine Aufgabe in einem Wettkampf zu erfüllen, muss Harry diesem Drachen in einer Arena ein Ei entwenden. Um überhaupt eine Chance gegen den wildgewordenen Feuerspeier zu haben, ruft der Jungzauberer  dazu mit einem einfachen Zauber seinen Flugbesen in die Arena. Die Wirkung des Spruchs: Der Besen saust von seinem Lagerplatz ausserhalb der Arena auf den Zauberstab und seinen Besitzer zu.

Diesen Kunstgriff kannst auch du ganz einfach nachmachen – vielleicht nicht mit einem Besen und nicht über eine so grosse Entfernung – aber mit einem einfachen Kunststoff-Zauberstab und Wasser. Und schon das wird deine Freunde verblüffen und vielleicht sogar zum Gruseln bringen!

Was du dazu brauchst

  • Einen Wasserhahn am Waschbecken oder einem Getränkespender – hauptsache, du kannst einen millimeterdünnen Wasserstrahl daraus fliessen lassen
  • Einen Kunststoff-Zauberstab (ein Spielzeug ist ebenso geeignet wie der Einweg-Plastiklöffel, den ich verwende – aber probiere das Experiment vor der grossen Aufführung aus, denn nicht jeder Kunststoff funktioniert gleich gut!)
  • Ein Kleidungsstück aus echter Wolle – zum Beispiel ein Schal, Wollhandschuhe oder eine Strickjacke. Besonders eindrücklich wirkt das Ganze, wenn das Woll-Stück Teil deines Kostüms ist.

Wie du den Zauber vorführst

  1. Öffne den Wasserhahn nur ein wenig, sodass so gerade eben ein stetiger, aber millimeterdünner Wasserstrahl herausläuft.
  2. Reibe deinen Zauberstab kräftig mit dem Kleidungsstück aus Wolle (ein guter Zauberer „beschäftigt“ sein Publikum währenddessen anderweitig, zum Beispiel im Gespräch).
  • Führe den Stab vorsichtig in die Nähe des Wasserstrahls und sprich „Accio Wasserstrahl!“. Berühre dabei in keinem Fall das Wasser mit dem Stab!
  • Der zuvor senkrecht fallende Strahl wird sich in Richtung des Stabes krümmen!
dünner Wasserstrahl und verhextes Wasser
Links: Ein dünner Wasserstrahl – Rechts: „Accio Wasserstrahl“ – deutliche Krümmung um einen elektrostatisch aufgeladenem Plastik-Löffelstiel!

Was dabei passiert

Letzte Woche habe ich ein Experiment gezeigt, das einen Hinweis darauf gibt, wie Wasser und andere Stoffe aufgebaut sind: Wasser besteht, wie andere Stoffe, aus ganz vielen winzig kleinen Teilchen. Die Wasserteilchen haben dabei eine besondere Eigenschaft: Sie sind elektrisch geladen!

Über elektrisch geladene Teilchen

Elektrisch geladene Teilchen spielen in unserem Alltag eine grosse Rolle. So fliessen solche Teilchen durch Stromkabel, wenn wir das Licht einschalten, und bringen die Lampe zum Leuchten. Diese Teilchen haben meist nur eine Ladung – und die ist positiv (+) oder negativ (-). Dafür, dass solche Teilchen überhaupt strömen, sorgt eine grundlegende physikalische Gesetzmässigkeit: Gleichartige Ladungen stossen sich ab, verschiedene Ladungen ziehen sich an. So bewegen sich die negativ geladenen „Strom-Teilchen“ oder „Elektronen“ vom negativ geladenen Minuspol einer Stromquelle weg und zum positiv geladenen Pluspol hin.


Wasserteilchen tragen dagegen zwei verschiedene Ladungen: Wie ein Magnet tragen sie an jeder Seite eine! (Da zwei verschiedene Ladungen einander aufheben, merkt man das den winzigen Wasserteilchen mit unseren groben Sinnen normalerweise nicht an.)

Wasserteilchen mit zwei Ladungs-Schwerpunkten
Ein Wasserteilchen trägt zwei elektrische Ladungen: Die negative Seite (-) ist rot, die positive Seite (+) ist blau schattiert.

Das führt dazu, dass die Plus-Seiten der Wasserteilchen die Minus-Seiten anziehen und umgekehrt. Im Wasser ordnen sich die Teilchen daher so, dass Plus-Seiten den Minus-Seiten gegenüber liegen und niemals gleiche Seiten einander zugewandt sind:

Wasserteilchen: Entgegengesetzte Ladungen ziehen sich an.

Der Kunststoffstab besteht dagegen zunächst aus ungeladenen Kunststoff-Teilchen. Durch das Reiben an der Wolle wird er jedoch aufgeladen (die Wolle übrigens auch – du kannst vielleicht die darauf folgenden Entladungen in der Wollkleidung knistern hören). Wenn er danach in die Nähe des Wasserstrahls kommt, ordnen sich die Wasserteilchen so, dass ihre dem Stab entgegengesetzt geladene Seite zum Stab weist. Die Anziehungskraft zwischen den verschiedenen Ladungen zieht die Teilchen so aus ihrer Flussrichtung – der Wasserstrahl krümmt sich in Richtung des Stabes!

Damit wünsche ich dir viel Spass beim Zaubern – und erzähl doch mal, wie es funktioniert hat!

Hast du das Experiment nachgemacht: 

[poll id=“34″]

Wenn etwas nicht oder nur teilweise funktioniert haben sollte, schreibt es in die Kommentare. Ich helfe gerne bei der Fehlersuche!

/8 Comments/by